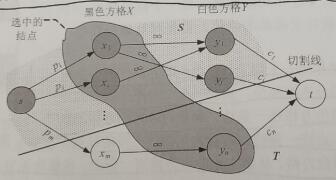
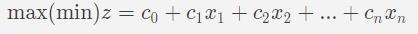最大收益问题 问题分析 经过分析,又根据最大流最小割定理,最大流的流值等于最小割容量。即:实验方案净收益=所有实验项目收益-最大流值。所以只需要求出最大流值即可、 算法设计 构建网络。根据输入的数据,添加源点和汇点,从源点s到每个实验项目Ei有一条有向边,容量是项目产生的收益pi。从每个实验仪器Ij到汇点t有一条有向边,容量是仪器费用cj,每个实验项目到该实验项目用到的仪器有一条有向边容量是 ∞,创建混合网络。 基于ISAP算法求网络最大流。 输出最大收益及实验方案。最大收益实验方案就是最小割中的S集合去掉源点。在…
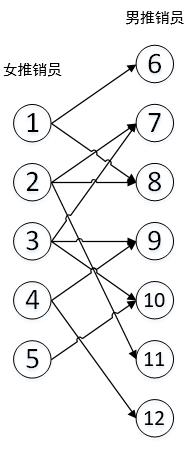
配对方案问题 问题分析 先了解几个概念。 二分图:又称二部图。设G=(V,E)是一个无向图,如果结点集V客分割为两个互不相交的子集(V1,V2),并且图中的每条边(i,j)所关联的两个结点i和j分别属于这两个不同的结点集(i∈V1,j∈V2),则称图G是一个二分图。 匹配:在图论中,一个匹配是一个边的集合,其中任意两条边都没有公共结点。 最大匹配:一个图所有匹配中,边数最多的匹配,成为这个图的最大匹配。 最佳推销员配对方案要求两个推销员男女搭配,相当于男女推销员形成了两个不相交的集合,可以配合工作的男女推销员有连线…
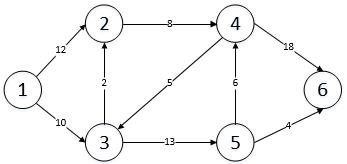
优化扩展——重贴标签算法ISAP 首先对所有的结点标记到汇点的最短距离,称之为高度。标高从汇点开始,用BFS方式,汇点的邻接点高度为1,继续访问的结点高度是2,一直到源点结束。 贴好标签之后,就可以从源点开始,沿着高度h(u)=h(v)+1且具有可行邻接边(cap>flow)的方向前进。我们找到了1-2-4-6。 我们再次从源点开始搜索,沿着高度h(u)=h(v)+1且具有可行邻接边(cap>flow)的方向前进,h(1)=3,h(2)=2,走到这里无法走到4号结点,因为没有邻接边,3号结点不近没有邻接边,而且高度…
线性规划问题 遇到一个线性规划问题,该如何解决呢? 1. 确定决策变量。 2. 确定目标函数。 3. 找出约束条件。 4. 求最优解。 一般线性规划问题可以表示为如下形式。 约束条件为: 变量满足约束条件的一组值成为线性规划问题的一个可行解。 所有可行解构成的集合成为线性规划的可行区域。 使目标函数取得极值的可行解称为最优解。 在最优解处目标函数的值成最优值。 线性规划解的情况: - 有唯一最优解。 - 有无数多个最优解。 - 没有最优解。 线性规划的标准型 标准型如下: 四个要求: 目标函数为最大值(即为max)…
最大网络流——最短增广路算法 问题描述 设有向带权图G=(V,E),V={s,v1,v2,v3,...,t}。在G中有两个特殊的结点s和t。s称为源点,t为汇点。图中各边的方向表示允许的流向,边上的权值表示该边允许通过的最大可能流量cap,且cap≥0,称它为边的容量。而且如果边集合E含有一条边(u,v),则比如不存在反方向的(v,u),我们称这样的有向带权图为网络。 网络是一个有向带权图,包含一个源点和一个汇点,没有反平行边。 网络流:网络流即网络上的流,是定义在网络边集E上的一个非负函数flow={flow(u…