最大网络流——最短增广路算法
问题描述
设有向带权图G=(V,E),V={s,v1,v2,v3,...,t}。在G中有两个特殊的结点s和t。s称为源点,t为汇点。图中各边的方向表示允许的流向,边上的权值表示该边允许通过的最大可能流量cap,且cap≥0,称它为边的容量。而且如果边集合E含有一条边(u,v),则比如不存在反方向的(v,u),我们称这样的有向带权图为网络。
网络是一个有向带权图,包含一个源点和一个汇点,没有反平行边。
网络流:网络流即网络上的流,是定义在网络边集E上的一个非负函数flow={flow(u,v)},flow(u,v)是边上的流量。
可行流:满足下面两个性质的网络流flow称为可行流:
1. 容量约束。每个管道的实际流量flow不能超过该管道的最大容量cap。
2. 流量守恒。除源点s和汇点t外,所有内部结点流入量=流出量。
网络最大流:在满足容量约束和流量守恒前提下,在流网络中找到一个净输出最大的网络流。
增广路算法(Ford-Fulkerson算法)
基本概念
1. 实流网络:实际流量的网络。
2. 残余网络:每个网络G及其上的一个流flow,都对应一个残余网络G。G和G结点集相同,而网络G中的每条边对应G中的一条边或两条边。在残余网络中,与网络边对应的同向边是可增量(即还可以增加多少),反向边是实际流量。
3. 可增广路是残余网络G中一条从源点s到汇点t的简单路径。
4. 可增广量是指在可增广路p上每条边可以增加的流量最小值。
可增广路增流
增流操作分为两个过程:一是在实流网络中增流;二是在残余网络中减流。
增广路算法
增广路定理:设flow是网络G的一个可行流,如果不存在从源点s到汇点t关于flow的可增广路,则flow是G的一个最大流。
增广路算法基本思想是在残余网络中找到可增广路,然后在实流网络中沿可增广路增流,在残余网络中沿可增广路减流;继续在残余网络中找可增广路,直到不存在可增广路为止。
最短增广路算法
Edmonds-Karp算法是以广度优先的增广路算法,又称为最短增广路算法(Shortest Augment Path, SAP)。算法步骤如下:
采用队列q来存放已访问未检查的结点。bool数组vis[]标注结点是否被访问过,pre[]数组记录可增广路上结点的前驱。pre[v]=u表示可增广路上v结点的前驱是u,最大流值maxflow=0。
- 初始化可行流flow为零流,即实流网络中全是零流边,残余网络中全是最大容量边。初始化vis[]=false,pre[]数组为-1。
- 令vis[s]=true,s加入队列q。
- 如果队列不空,继续下一步,否则算法结束,找不到可增广路。当前的实流网络就是最大流网络,返回最大流值maxflow。
- 队头元素new出队,在残余网络中检查new的所有邻接结点i。如果未被访问,则访问它,令vis[i]=true,pre[i]=new;如果i=t,说明已经到达汇点,找到一条可增广路,转向第5步;否则结点i加入队列q,,转向第3步。
- 从汇点开始,通过前驱数据pre[],逆向找可增广路上每条边值的最小值,即可增量d。
- 在实流网络中增流,在残余网络中减流,maxflow+=d,转向第2步。
算法设计
在求解的时候需要先初始化一个可行流,然后在可行流上不断找可增广路增流即可。初始化为任何一个可行流都可以,但需要满足容量约束和平衡约束。通常初始化可行流为0流。
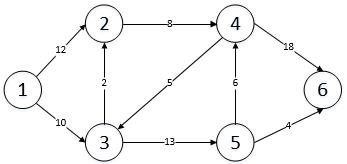
- 数据结构。网络G邻接矩阵为g[][]。
| ∞ | 12 | 10 | ∞ | ∞ | ∞ |
|---|---|---|---|---|---|
| ∞ | ∞ | ∞ | 8 | ∞ | ∞ |
| ∞ | 2 | ∞ | ∞ | 13 | ∞ |
| ∞ | ∞ | 5 | ∞ | ∞ | 18 |
| ∞ | ∞ | ∞ | 6 | ∞ | 4 |
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
- 初始化。初始化可行流flow为零流,即实流网络中全是零流边,残余网络全是最大容量边,初始化vis[]=false,pre[]数组为-1。
| vis[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0|0 |
| pre[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| -1 | -1 | -1 | -1 | -1 | -1 |
- 令vis[1]=true,1加入队列q。
- 队头元素1出队。在残余网络G*中依次检查1的所有邻接结点2和3,两个结点都未被访问,令vis[2]=true,pre[2]=1,结点2加入队列q;vis[3]=true,pre[3]=1,结点3加入队列q。此时vis[i]、pre[i]和q如下所示。
| vis[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0|0 |
| pre[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| -1 | 1 | 1 | -1 | -1 | -1 |
| 序号 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| q | 2 | 3 |
- 队头元素2出队。在残余网络中依次检查2的所有邻接结点4,4未被访问,令vis[4]=1,pre[4]=2,结点4加入队列q。
- 队头元素3出队。在残余网络中依次检查3的所有邻接结点2和5。2已经被访问,5未被访问,令vis[5]=1,pre[5]=3,结点5加入队列q。此时vis[i]、pre[i]和q如下所示。
| vis[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0|0 |
| pre[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| -1 | 1 | 1 | 2 | 3 | -1 |
| 序号 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| q | 4 | 5 |
- 队头元素4出队。在残余网络中依次检查4的所有邻接结点3和6。3已经被访问,6未被访问,令vis[6]=1,pre[6]=4。结点6就是汇点,找到一条增广路。此时vis[i]、pre[i]和q如下所示。
| vis[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1|1 |
| pre[i] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| -1 | 1 | 1 | 2 | 3 | 4 |
| 序号 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| q | 5 |
- 读取钱取数组,得到1-2-4-6,找到该路径上的最小边值为8,即可增量d=8。
- 实流网络增流,残余网络减流。可增广路通向的边增流d,反向边减流d。
- 重复2~8步,找到第2条可增广路1-3-5-6,找到最小边值,即可增量=4,进行第9步。
- 重复2~8步,找到第3条可增广路1-3-5-4-6,找到最小边值,即可增量=6,进行第9步。
- 重复2~8步,找不到可增广路,算法结束,最大流值为所有的增量之和18。
为什么要采用残余网络+实流网络?
在网络G及可行流直接找可增广路,有可能得不到最大流。
为什么要用实流网络?
从残余网络中无法判断哪些是实流边,哪些是可增量边,如果想知道实际的网络流量,就需要借助于实流网络。
整个过程是采用:在残余网络找可增广路,在实流网络中增流相结合的方式,求解最大流。
代码实现
1.找可增广路。采用普通队列实现对残余网络的广度搜索,从源点u开始,s搜索邻接点v。如果v被访问,则标记已访问,且记录v结点的前驱为u;如果u结点不是汇点则入队;如果u结点恰好是汇点,则返回,找到汇点时则找到一条可增广路。如果队列为空,则说明已经找不到可增广路。
bool bfs(int s,int t)
{
memset(pre,-1,sizeof(pre));
memset(vis,false,sizeof(vis));
queue<int>q;
vis[s]=true;
q.push(s);
while(!q.empty())
{
int now=q.front();
q.pop();
for(int i=1;i<=n; i++)//寻找可增广路
{
if(!vis[i]&&g[now][i]>0)//未被访问且有边相连
{
vis[i] = true;
pre[i] = now;
if(i==t) return true;//找到一条可增广路
q.push(i);
}
}
}
return false;//找不到可增广路
}
2.沿可增广路增流。根据钱取数组,从汇点向前,一直到源点,找到可增广路上所有边的最小值,即为可增量d。然后从汇点向前,一直到源点,残余网络中同向边减流,反向边增流,实流网络中如果是反向边,则减流,否则正向边增流。
int EK(int s, int t)
{
int v,w,d,maxflow;
maxflow = 0;
while(bfs(s,t))//可以增广
{
v=t;
d=INF;
while(v!=s)//找可增量d
{
w=pre[v];//w记录v的前驱
if(d>g[w][v])
d=g[w][v];
v=w;
}
maxflow+=d;
v=t;
while(v!=s)//沿可增广路增流
{
w=pre[v];
g[w][v]-=d; //残余网络中正向边减流
g[v][w]+=d; //残余网络中反向边增流
if(f[v][w]>0) //实流网络中如果是反向边,则减流,否则正向边增流
f[v][w]-=d;
else
f[w][v]+=d;
v=w;
}
}
return maxflow;
}
3.输出实流网络
void print()//输出实流网络
{
cout<<endl;
cout<<"----------实流网络如下:----------"<<endl;
cout<<" ";
for(int i=1;i<=n;i++)
cout<<setw(7)<<"v"<<i;
cout<<endl;
for(int i=1;i<=n;i++)
{
cout<<"v"<<i;
for(int j=1;j<=n;j++)
cout<<setw(7)<<f[i][j]<<" ";
cout<<endl;
}
}
算法复杂度分析
- 时间复杂度:找到一条可增广路时间是O(E),最多会执行O(VE)此,因此关键边总数为O(VE),因此总的时间复杂度为O(VE2)。其中V为结点个数,E为边的数量。
- 空间复杂度:使用了一个二维数组,所以复杂度为O(V2)。


文章评论