摘要

传统方法通常使用时频掩码（TF mask）对含噪频谱图进行点乘处理，而复数值掩码（CM）因其能修正相位而优于时值掩码。近期很多研究提出使用复数值滤波器代替掩码点乘操作，通过利用频带内局部时间相关性，整合过去和未来时间步的信息。
这篇论文提出了DeepFilterNet，是一种基于深度滤波的两阶段语音增强框架。第一阶段利用ERB（等效矩形带宽）缩放的增益增强语音的频谱包络，模拟人耳听觉的频率感知特性；第二阶段通过深度滤波增强语音的周期性成分，除了利用语音的感知特性外，还通过可分离卷积和线性层/循环层中的分组策略强制网络稀疏化，以设计低复杂度架构。

引言

现有的很多方法通常在STFT后通过深度神经网络估计时频掩码，包括时值掩码和复数值掩码。但是当分辨率过低的时候，这些方法难以消除语音谐波间的噪声。传统方法需要至少20ms的时间窗，对应50Hz的最低频率分辨率。
为什么频率分辨率过低的时候，时值掩码和复数值掩码无法有效去除语音谐波间的噪声？
  1. 谐波与噪声在频域的重叠
    1. 语音谐波特性：浊音（如元音）的频谱由基频（f0）及其整数倍谐波（2f0,3f0,…）构成。相邻谐波间隔为基频（f0），成年男性基频约为 85 Hz，女性约为 200 Hz。
    2. 低频率分辨率的影响： 当STFT的FFT窗口较短（如 20 ms，对应频率分辨率 50 Hz）时，每个频带的带宽较大（如 50 Hz）。若相邻谐波间隔（如 100 Hz）小于频带带宽，多个谐波可能落入同一频带。此时，噪声（如白噪声）可能填充在谐波间的间隙中，但因频带较宽，噪声与谐波在时频域混叠，无法通过简单的掩码区分。
  2. 掩码的局限性
      时频掩码在语音增强中用于调整每个时频单元的能量，抑制噪声部分。时值掩码（比如幅度掩码）主要调整幅度，而复数值掩码可以同时调整幅度和相位。
    1. 时值掩码（幅度掩码）
      1. 仅调整幅度：时值掩码通过抑制含噪频带的幅度来增强语音，但无法修正相位。在低分辨率下，谐波与噪声在频带内混合，幅度掩码会同时削弱谐波和噪声，导致语音失真或残留噪声。
      2. 相位不匹配：噪声相位与语音相位在混合后可能破坏语音的相干性，仅调整幅度无法恢复干净的相位信息。
    2. 复数值掩码（CRM）
      1. 相位修正能力有限：复数值掩码通过复数乘法同时调整幅度和相位，但若频带内信号已严重混叠（如谐波与噪声重叠），相位修正难以分离二者。
      2. 局部相关性缺失：传统掩码独立处理每个时频单元（TF-bin），未利用相邻时频单元的相关性。而噪声在谐波间可能呈现非平稳特性，局部相关性建模不足会导致残留噪声。
本论文能解决以上问题的原因是：
  1. 跨时频单元的滤波： DF利用复数值滤波器（公式3），对当前时频单元及其相邻单元（时间轴）进行线性组合。即使频带较宽，DF仍可通过局部时间相关性增强周期性成分（如谐波），抑制非周期性噪声。
  2. 周期性分量增强： 语音谐波在低频段（如 <5 kHz<5kHz）能量集中且周期性显著。DF通过建模相邻帧的谐波结构，能够从混叠信号中提取周期性成分，而传统掩码缺乏这种跨帧建模能力。
  3. 自适应权重控制： 通过可学习权重 α(k)（公式4），DF动态选择增强后的信号（$$Y^{DF′}$$）或保留ERB增益结果（$$Y^G$$），避免在噪声主导区域引入伪影。
这篇论文提出了一种深度滤波的语音增强框架，结合时值增益和深度滤波增强模块。第一级利用语音和噪声的平滑频谱包络特性，通过ERB滤波器组将输入输出维度降低至32个频带，构建低计算成本的编码器/解码器网络。由于ERB滤波器组的最小带宽（100~250Hz）不足以增强周期性成分，第二级通过深度滤波估计低频带（<=5kHz）的复数值滤波器系数，以增强语音的周期性成分。由于周期性语音成分的大部分能量集中在较低频率，深度滤波（DF）增强仅应用于较低频率。
本文证明深度滤波在5ms至30ms的多种FFT窗口下均优于复数值比率掩码（CRM），并在5ms低延迟（频率分辨率250Hz）条件下仍能有效增强语音周期性成分。深度滤波通过跨时频单元的滤波操作可恢复信号中缺口滤波或时帧置零等失真。
什么是ERB滤波器组？
ERB（Equivalent Rectangular Bandwidth Filter Bank）是一种在音频处理、语音识别等领域广泛应用的滤波器组。
基本概念：ERB 滤波器组是一组具有特定频率响应特性的滤波器集合。其设计基于听觉感知原理，模拟了人类听觉系统对不同频率声音的感知特性。在人类听觉系统中，不同频率的声音会在耳蜗中引起不同位置的振动，从而被感知为不同的音调。ERB 滤波器组就是试图模仿这种频率分析特性，将输入的音频信号在不同的频率通道上进行分解。
原理基础：其原理基于等效矩形带宽（ERB）的概念。等效矩形带宽是指一个理想矩形滤波器的带宽，该矩形滤波器在特定频率处具有与实际滤波器相同的能量传递特性。ERB 滤波器的带宽不是固定的，而是随着中心频率的变化而变化，一般来说，中心频率越高，带宽越宽，这种特性与人类听觉系统对高频声音分辨率相对较低、对低频声音分辨率相对较高的特点相符合。
数学表达：在数学上，ERB 与中心频率f之间的关系可以用这个公式近似表示：
ERB=24.7(4.37f/1000+1)
其中f单位是Hz，这个公式描述了每个ERB滤波器的带宽如何随着中心频率变化。对于一个 ERB 滤波器组，通常会有多个中心频率不同的滤波器，每个滤波器的频率响应可以用相应的数学函数来描述，例如可以用高斯函数等函数形式来构建 ERB 滤波器的频率响应曲线，以实现对不同频率成分的选择性滤波。

DEEPFILTER NET

设含噪混响信号为
$$x(t)=s(t)*h(t)+z(t)\quad\quad\quad\quad(1)$$
转换为频域则为：
$$X(k,f)=S(k,f)⋅H(k,f)+Z(k,f) \quad\quad\quad\quad(2)$$
深度滤波在时频域定义为复数值滤波器：
$$Y(k, f)=\sum_{i=0}^{N} C(k, i, f) \cdot X(k-i+l, f)\quad\quad\quad\quad(3)$$
在我们框架后，深度滤波器应用于增益增强后的频谱图。引入可学习权重控制最终输出：

$$Y^{D F}(k, f)=\alpha(k) \cdot Y^{D F^{\prime}}(k, f)+(1-\alpha(k)) \cdot Y^{G}(k, f)\quad\quad\quad\quad(4)$$

框架概述

给定带噪语音信号x(t)，经过STFT后的频域信号为X(k,f)。此框架可以支持最高48kHz的采样率，STFT的窗长N_FFT为5ms到30ms之间。默认情况下，我们使用的50%的overlap，但是也支持更高的overlap。我们为深度神经网络使用两种类型的输入特征。对于ERB编码器和解码器特征X_{ERB}(k,b),b ∈ [0,N_{ERB},我们计算对数功率谱图，用使用衰减时间为 1 秒的指数均值归一化方法对其进行归一化处理，并应用一个可配置频段数量N_{ERB}的ERB滤波器组。
对于深度滤波器X_DF(k,f’), f’ ∈[0,f_{DF}，我们使用复频率谱图作为输入，同时并使用具有相同衰减参数的指数单位归一化方法对其进行归一化处理。
我们采用编码器 / 解码器架构来预测经等效矩形带宽（ERB）缩放后的增益。在将这些增益与含噪频谱图逐点相乘之前，会应用逆 ERB 滤波器组将增益转换回频域。为了进一步增强周期性的成分，DeepFilterNet回预测阶数为N的各频段滤波器系数C^N。我们仅在频率小于等于f_{DF}的频段应用深度滤波，这是因为假定周期性成分的大部分能量都集中在较低频率范围内。结合卷积层中的深度神经网络（DNN）前瞻以及深度滤波器前瞻，整体延迟由l_{N_{FFT}}+max(l_{DNN},l_{DF})给出。对于如果N_{FFT}=24的情况，最小延迟为5+max(0,0)=5毫秒（240/48000*1000=5ms)。

DNN模型

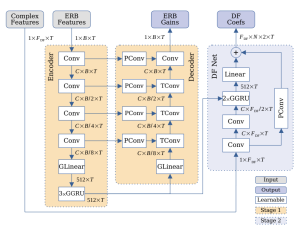
本文使用一个仅使用标准神经网络层（如卷积层、批量归一化层、修正线性单元（ReLU）激活函数等）的高效DNN，这样既能利用层融合技术，又能借助推理框架的良好支持。本文实际使用的是一个UNet网络结构，如图2所示。卷积块由一个可分离卷积（深度可分离卷积后面接一个1×1卷积）组成，卷积核大小为（3×2），通道数为C=64。然后是批量归一化层和ReLU激活函数。卷积层在时间上是对齐的，因此第一层可能会引入一个整体前瞻l_{DNN}。其余的卷积层都是因果的，不会再增加额外的延迟。同时在全连接层和门控循环单元（GRU）层大量使用分组技术。也就是说，层输入被划分为 P = 8个组，这会得到P 个更小的门控循环单元（GRU）层 / 全连接层，其隐藏层大小为(512/P = 64)。输出会进行混洗操作，以恢复组间相关性，然后再次拼接成完整的隐藏层大小。另外，使用带有跳跃连接相加（add – skip）的卷积路径被用于保留频率分辨率。
本文为深度滤波网络（DF Net）使用全局路径跳跃连接，以便在输出层很好地呈现原始含噪相位的特征。

数据预处理

训练时采用动态增强：
  • 混合纯净语音与5种噪声（SNR: -5~40dB）。
  • 添加二阶滤波、均衡器（EQ）、随机增益（-6~6dB）。
  • 随机重采样和房间脉冲响应（RIR）模拟混响。
  • 支持全频带（48kHz）训练，兼容低采样率输入。

损失函数

要提供理想的深度滤波（DF）系数C^N并非易事，因为存在无数种可能性。相反，本文采用压缩频谱损失来隐式学习等效矩形带宽（ERB）增益G和滤波系数C^N。
$$\mathcal{L}_{spec}=\sum_{k,f}\left \| |Y|^c-|S|^c \right \|^2+\sum_{k,f}\left \| \left | Y \right |^ce^{j\varphi Y}-|S|^ce^{j\varPhi S} \right \|^2\quad\quad\quad\quad(5)$$
其中，c=0.6是一个用于对感知响度进行建模的压缩因子。同时包含幅度项和相位感知项，使得这种损失函数适用于对实值增益和复数深度滤波（DF）系数预测进行建模。为了增强幅度接近零的时频（TF）单元的梯度（例如对于采样率较低的输入信号），我们采用类似下面的角度反向传播方法来计算：
在这里R{X}和S{X}分别代表了X的实部和虚部，并且$$|X_h|^2=max(R\{X\}^2+S\{X\}^2,1e^{-12})$$是经过强化处理的幅度平方值，用以避免出现除以 0 的情况。作为一个额外的损失项，我们强制深度滤波（DF）分量仅增强信号的周期性部分。这么做的动机如下：对于纯噪声部分，与等效矩形带宽（ERB）增益相比，深度滤波没有任何优势。深度滤波甚至可能会因为对发动机噪声或嘈杂人声等周期性噪声进行建模而产生伪影，这在衰减受限模型中最为明显。此外，对于仅包含随机分量（如摩擦音或爆破音）的语音，深度滤波也没有任何作用。假设这些部分的大部分能量集中在较高频率，我们会计算低于 f_{DF}频率处的局部信噪比。因此，可由以下方式得出:
联合损失函数包括频谱损失和周期性约束损失：
$$\mathcal{L}=\lambda_{spec}\mathcal{L}_{spec}(Y,S)+\lambda _{\alpha }\mathcal{L}_{\alpha }\quad\quad\quad\quad(8)$$
受编辑器限制，部分内容展现不正确，可直接访问源文档：
访问密码：52991H5&