最大收益问题

问题分析

经过分析，又根据最大流最小割定理，最大流的流值等于最小割容量。即：实验方案净收益=所有实验项目收益-最大流值。所以只需要求出最大流值即可、

算法设计

1. 构建网络。根据输入的数据，添加源点和汇点，从源点s到每个实验项目E_i有一条有向边，容量是项目产生的收益p_i。从每个实验仪器I_j到汇点t有一条有向边，容量是仪器费用c_j，每个实验项目到该实验项目用到的仪器有一条有向边容量是
   ∞，创建混合网络。
2. 基于ISAP算法求网络最大流。
3. 输出最大收益及实验方案。最大收益实验方案就是最小割中的S集合去掉源点。在最大流对应的混合网络中，从选点开始，沿着cap>flow的边深度优先遍历，遍历到的结点就是S集合，即对应的实验项目和仪器就是选中的实验方案。

代码实现

1. 输出最大收益方案

void DFS(int s)//深度搜索最大获益方案{ for(int i=V[s].first;~i;i=E[i].next)//读当前结点的邻接表 if(E[i].cap>E[i].flow) { int u=E[i].v; if(!flag[u]) { flag[u]=true; DFS(u); } }}void print(int m,int n)//输出最佳方案{ cout<<"----------最大获益方案如下：----------"<<endl; DFS(0); cout<<"选中的实验编号："<<endl; for(int i=1;i<=m;i++) if(flag[i]) cout<<i<<" "; cout<<endl; cout<<"选中的仪器编号："<<endl; for(int i=m+1;i<=m+n;i++) if(flag[i]) cout<<i-m<<" ";}

2. 构建混合网络

cout<<"请输入实验数m和仪器数n:"<<endl; cin>>m>>n; init(); total=m+n; cout<<"请依次输入实验产生的效益和该实验需要的仪器编号(为0结束):"<<endl; for(int i=1;i<=m;i++) { cin>>cost; sum+=cost; add(0, i, cost);//源点到实验项目的边，容量为该项目效益 while(cin>>num,num) //num为该项目需要的仪器编号 add(i, m+num, INF);//实验项目到需要仪器的边，容量为无穷大 } cout<<"请依次输入所有仪器的费用:"<<endl; for(int j=m+1;j<=total;j++) { cin>>cost; add(j, total+1, cost);//实验仪器到汇点的边，容量为实验仪器费用 }

算法复杂度

时间复杂度：找到一条可增广路时间为O(V)，最多会执行O(VE)次，因为关键边的总数为O(VE)，因此总的时间复杂度为O(V²E)，其中V为结点个数，E为边的数量。

空间复杂度O(V)。

方格取数问题

问题简介

从一个矩阵中选取一些数，要求满足任意两个数不相邻，使这些数的和最大。实际上就是讲矩阵中的数分为两部分，对矩阵中的点进行黑白着色。

问题分析

黑色方格作为一个集合X，白色方格作为一个集合Y，可以将一个图分为两部分，构成一个二分图。添加源点和汇点，从源点向黑色方格连一条边，容量为该黑色方格的权值，从白色方格向汇点连一条边，容量为该白色方格的权值，对于每一对相邻的黑白方格，从黑方格向白方格连一条边，容量为无穷大。

同样是求出最小割，选中方格的最大权值=所有方格权值之和-最小割容量。

算法设计

1. 构建网络
2. 求网络最大流。
3. 输出选中物品的最大价值、物品选择方案。

选中物品的最大价值=所有物品价值之和-最大流值
注意：切割线切到的边容量是没选中的方格权值。

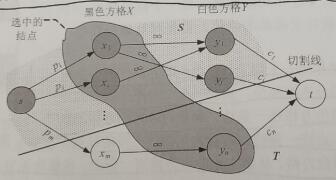
物品选择方案就是最小割中的S集合中的黑色方格和T集合中的白色方格。找到最小割后，从源点出发，沿着cap>flow的边DFS，遍历到的结点就是S集合，没有遍历到的结点就是T集合。输出S集合中的黑色方格和T集合中的白色方格。如上图所示。

算法详解

假设整个图如下图所示。

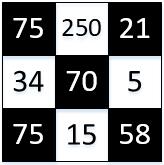
1. 构建网络，根据输入的数据，绘制二分图，添加源点s和汇点t，从黑方格向白方格连一条边，容量为∞，创建网络。

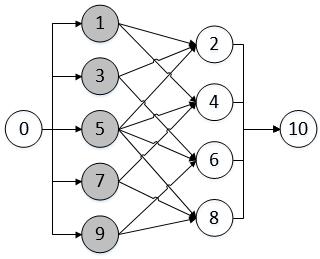
2. 在混合网络上用ISAP算法求网络最大流，找到如下6条增广路径。
   • 增广路径：10-6-9-0.增流5。
   • 增广路径：10-8-9-0.增流15。
   • 增广路径：10-4-7-0.增流34。
   • 增广路径：10-2-5-0.增流70。
   • 增广路径：10-2-3-0.增流21。
   • 增广路径：10-2-1-0.增流75。

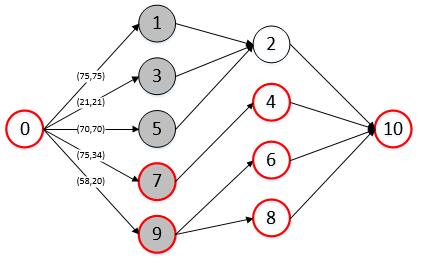
切割线中被选中的就是红色圈圈的结点，选择的道路是从源点出发，按照cap>flow的结点（这里面只有7和9两个结点）去深度遍历，这就是S集合；1、3、5和2是T集合。
所以选中的黑点为7、9，白色为2。

代码实现

（1）构建网络

//创建混合网络for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) { if((i+j)%2==0)//染黑色 { add(0,(i-1)*n+j,map[i][j]);//从源点到当前物品加边，容量为物品价值 flag[(i-1)*n+j]=1;//染色 //当前物品结点到四个相邻物品结点发出一条有向边，容量为无穷大 for(int k=0;k<4;k++) { int x=i+dir[k][0]; int y=j+dir[k][1]; if(x<=m && x>0 && y<=n && y>0) add((i-1)*n+j,(x-1)*n+y,INF); } } else //染白色，也就相当于flag为0，不需要专门的语句 //从源点到当前物品加边，容量为物品价值 add((i-1)*n+j,total+1,map[i][j]); }

（2）输出挑选物品的最大价值

cout<<"挑选物品的最大价值："<<sum-Isap(0,total+1,total+2)<<endl;

（3）输出选中的物品编号。

void DFS(int s){ //读取当前结点的邻接表 for(int i=V[s].first;~i;i=E[i].next) { if(E[i].cap>E[i].flow) { int u=E[i].v; if(!dfsflag[u]) { dfsflag[u]=true; DFS(u); } } }}//输出最佳方案void print(int m,int n){ cout<<"-----最佳方案：-----"<<endl; cout<<"选中物品编号<<endl; DFS(0); for(int i=1;i<=m*n;i++) if(())}

算法复杂度

时间复杂度：找到一条可增广路时间为O(V)，最多会执行O(VE)次，因为关键边的总数为O(VE)，因此总的时间复杂度为O(V²E)，其中V为结点个数，E为边的数量。

空间复杂度O(V)。

旅游路线问题

问题分析

给定一张地图，图中结点代表景点，边代表景点可以直达。现要求找到满足下面要求且途径景点最多的一条旅游线路：

1. 从最东端起点出发，从东往西经过若干个景点到达最西端的景点，然后再从西向东回到家（可途径若干景点）；
2. 除起点外，任何景点只能访问1次。

算法设计

1. 构建网络。根据输入的数据，按顺序对景点进行编号，即景点i对应结点i，对每个结点拆点，拆为两个结点i和i’，且从i到i’连接一条边，边容量为1，单位流量费用为0；源点和终点拆点时，边的容量为2，单位流量费用为0；如果景点i到景点j可以直达，则从结点i’到结点j连接一条边，边的容量为1，单位流量费用为-1，创建混合网络。
2. 求网络最小费用最大流。
3. 求出最优的旅游线路。从源点出发，沿着flow>0且cost≤0的方向深度优先遍历，到达终点后，再沿着flow＜0且cost≥0的方向深度优先遍历，返回源点。

代码实现

1. 构建网络

cout<<"请输入景点个数n和直达线路数m:"<<endl; cin>>n>>m; init();//初始化 maze.clear(); cout<<"请输入景点名str"<<endl; for(i=1;i<=n;i++) { cin>>str[i]; maze[str[i]]=i; if(i==1||i==n) add(i,i+n,2,0); else add(i,i+n,1,0); } cout<<"请输入可以直达的两个景点名str1,str2"<<endl; for(i=1;i<=m;i++) { cin>>str1>>str2; int a=maze[str1],b=maze[str2]; if(a<b) { if(a==1&&b==n) add(a+n,b,2,-1); else add(a+n,b,1,-1); } else { if(b==1&&a==n) add(b+n,a,2,-1); else add(b+n,a,1,-1); } }

2. 求网络最小费用最大流

bool SPFA(int s, int t, int n)//求最小费用路的SPFA{ int i, u, v; queue <int> qu; // 队列，STL实现 memset(vis,0,sizeof(vis));//访问标记初始化 memset(c,0,sizeof(c)); //入队次数初始化 memset(pre,-1,sizeof(pre)); //前驱初始化 for(i=1;i<=n;i++) { dist[i]=INF; //距离初始化 } vis[s]=true; //结点入队vis要做标记 c[s]++; //要统计结点的入队次数 dist[s]=0; qu.push(s); while(!qu.empty()) { u=qu.front(); qu.pop(); vis[u]=false; //队头元素出队，并且消除标记 for(i=V[u].first; i!=-1; i=E[i].next)//遍历结点u的邻接表 { v=E[i].v; if(E[i].cap>E[i].flow && dist[v]>dist[u]+E[i].cost)//松弛操作 { dist[v]=dist[u]+E[i].cost; pre[v]=i; //记录前驱 if(!vis[v]) //结点v不在队内 { c[v]++; qu.push(v); //入队 vis[v]=true; //标记 if(c[v]>n) //超过入队上限，说明有负环 return false; } } } } cout<<"最短路数组"<<endl; cout<<"dist[ ]="; for(int i=1;i<=n;i++) cout<<" "<<dist[i]; cout<<endl; if(dist[t]==INF) return false; //如果距离为INF，说明无法到达，返回false return true;}int MCMF(int s,int t,int n) //minCostMaxFlow{ int d; //可增流量 maxflow=mincost=0;//maxflow 当前最大流量，mincost当前最小费用 while(SPFA(s,t,n))//表示找到了从s到t的最短路 { d=INF; cout<<endl; cout<<"增广路径："<<t; for(int i=pre[t]; i!=-1; i=pre[E[i^1].v]) { d=min(d, E[i].cap-E[i].flow); //找最小可增流量 cout<<"--"<<E[i^1].v; } cout<<"增流："<<d<<endl; cout<<endl; for(int i=pre[t]; i!=-1; i=pre[E[i^1].v])//修改残余网络，增加增广路上相应弧的容量，并减少其反向边容量 { E[i].flow+=d; E[i^1].flow-=d; } maxflow+=d; //更新最大流 mincost+=dist[t]*d; //dist[t]为该路径上单位流量费用之和 ，最小费用更新 } return maxflow;}

3. 输出最优的旅游路线

void print(int s,int t){ int v; vis[s]=1; for(int i=V[s].first;~i;i=E[i].next) if(!vis[v=E[i].v]&&((E[i].flow>0&&E[i].cost<=0)||(E[i].flow<0&&E[i].cost>=0))) { print(v,t); if(v<=t) cout<<str[v]<<endl; }}