线性规划问题
遇到一个线性规划问题,该如何解决呢?
1. 确定决策变量。
2. 确定目标函数。
3. 找出约束条件。
4. 求最优解。
一般线性规划问题可以表示为如下形式。
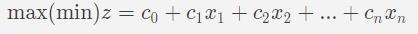
约束条件为:
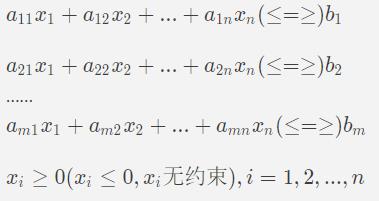
- 变量满足约束条件的一组值成为线性规划问题的一个可行解。
- 所有可行解构成的集合成为线性规划的可行区域。
- 使目标函数取得极值的可行解称为最优解。
- 在最优解处目标函数的值成最优值。
线性规划解的情况:
- 有唯一最优解。
- 有无数多个最优解。
- 没有最优解。
线性规划的标准型
标准型如下:
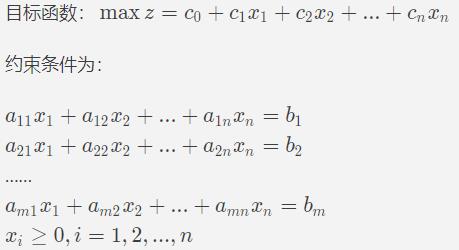
四个要求:
- 目标函数为最大值(即为max);
- 约束条件常数项bi>=0;
- 约束条件全部为等式约束;
- 决策变量xi非负约束。
线性规划标准型转化方法:
- 一般线性规划行驶中目标函数如果求最小值,那么令z'=-z,得到最优解后,加负号即可。
- 右端常数项小于零时,则不等式两边同乘-1,将其变成大于零;同时改变不等号的方向,保证恒等变形。
- 约束条件为大于与等于约束条件时,则在不等式左侧减去一个新的非负变量将不等式约束改为等式约束。例如2x1-3x2≥10,修改为:2x1-3x2-x3=10,x3>0。
- 约束条件为小于等于约束时,则在不等式左侧加去一个新的非负变量将不等式约束改为等式约束。
- 无约束的决策变量x,即可正可负的变量,则引入两个新的非负变量x'和x'',令x-x'-x'',其中x'≥0,x''≥0,将x带入线性规划模型。例如:2x1-3x2+x3=10,x3无约束,则可以修改为:x3=x4-x5,x4>0,x5>0,带入方程得到2x1-3x2+x4-x5=10,x4>0,x5>0。
注意:引入的新的非负变量称为松弛变量。
单纯形算法图解
基本概念:
- 基本变量:每个约束条件中的系数为正,且只出现在一个约束条件中的变量。
- 非基本变量:除基本变量以外的变量。
- 基本可行解:满足标准形式约束条件的可行解称为基本可行解。
- 检验数:目标函数中非基本变量的技术。
基本定理:
- 最优解判别定理:若目标函数中关于非基本变量的所有系数小于等于0,则当前基本可行解就是最优解。
- 无穷多最优解判别定理:若目标函数中关于费基本变量的所有检验数小于等于0,同时存在某个非基本变量的检验数等于0,则线性规划问题有无穷多个最优解。
- 无界解定理:如果某个检验数cj大于0,而cj所对应的列向量的各分量a1j,a2j,...,amj都小于等于0,则该线性规划问题有无界解。
约束标准型线性规划问题单纯形算法步骤如下:
- 建立初始单纯形表。找出基本变量和非基本变量,将目标函数由非基本变量表示,建立初始单纯形表。注意:如果目标函数含有基本变量,要通过约束条件方程转换为非基本变量。 还要注意:基本变量的系数要转化为1 ,否则不能按照下面的计算方法。基本变量做行,非基本变量做列,检验数放第一行,常数项放低1列,约束条件中非基本变量的系数作为值,构造初始单纯形表。如下所示:
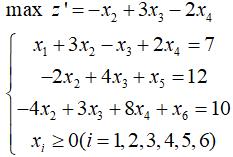
| b | x2 | x3 | x4 | |
|---|---|---|---|---|
| c | 0 | -1 | 3 | -2 |
| x1 | 7 | 3 | -1 | 2 |
| x5 | 12 | -2 | 4 | 0 |
| x6 | 10 | -4 | 3 | 8 |
- 判断是否得到最优解。判别并检查目标函数的所有系数。
- 如果所有的cj<=0,则已经获得最优解,算法结束。
- 若在检验数cj中,有些为正数,但其中某一正的检验数所对应的列向量的各分量均小于等于0,则线性规划问题无界,算法结束。
- 若在检验数cj中,有些为正数且它们对应的列向量中有正的分量,则转到第3步。
- 选入基变量。选取所有正检验数中最大的一个,记为ce,其对应的非基本变量为xe,称为入基变量,xe对应的列向量[a1e,a2e,...,ame]T为入基列。在本例中,x3为入基变量,x3对应的列向量为入基列,如下所示。
| b | x2 | x3 | x4 | |
|---|---|---|---|---|
| c | 0 | -1 | 3 | -2 |
| x1 | 7 | 3 | -1 | 2 |
| x5 | 12 | -2 | 4 | 0 |
| x6 | 10 | -4 | 3 | 8 |
- 选离基变量、选取“常数列元素/入基列元素”正比值最小者,所对应的基本变量xk为离基变量。xk对应的行向量为离基行。在本例中,x5为离基变量,对应的行向量为离基行。
- 换基变换。在单纯形表上将入基变量和离基变量互换位置,即在本例中将x3和x5交换位置,换基变换后如下所示。
| b | x2 | x5 | x4 | |
|---|---|---|---|---|
| c | 0 | -1 | 3 | -2 |
| x1 | 7 | 3 | -1 | 2 |
| x3 | 12 | -2 | 4 | 0 |
| x6 | 10 | -4 | 3 | 8 |
- 计算新的单纯形表。按照下面的方法计算新的单纯形表,然后转第2步。4个特殊位置如下:
- 入基列:-原值/交叉位值(不包括交叉位)。
- 离基行=原值/交叉位值(不包括交叉位)
- 交叉位=原值取倒数。
- c0位:原值+同行入基列元素*同列离基行元素/交叉位值。
- 一般位置元素=原值-同行入基列元素*同列离基行元素/交叉位值。
| b | x2 | x5 | x4 | |
|---|---|---|---|---|
| c | 9 | 0.5 | -0.75 | -2 |
| x1 | 10 | 2.5 | 0.25 | 2 |
| x3 | 3 | -0.5 | 0.25 | 0 |
| x6 | 1 | -2.5 | -0.75 | 8 |
- 判断是否得到最优解,若没有继续第3~6步,直到找到最优解或判定无界解停止。在本例中,再次选定基列变量x2和离基变量x1,将他们互换位置,重新计算单纯形表,得到下面的表。
| b | x1 | x5 | x4 | |
|---|---|---|---|---|
| c | 11 | -0.2 | -0.8 | -2.4 |
| x2 | 4 | 0.4 | 0.1 | 0.8 |
| x3 | 5 | 0.2 | 0.3 | 0.4 |
| x6 | 11 | 1 | -0.5 | 10 |
可以看出目标函数的检验数全部都小于0,得到最优解。c0就是我们要的最优值(11),而最优解是由基本变量对应的常数项组成的,即x2=4,x3=5,x6=11,非基本变量全部置零。以上算法获得的是max z',而本题要求是min z,所以答案是-11。
工厂最大效益——单纯形算法
题目描述
某食品加工厂有三个车间,第一车间用1个单位的原料N可以加工5个单位的产品A或者2个单位的产品B。产品A若直接出售,价格10元,如果第二车间继续加工,加工费5元,加工后售价19元,产品B直接出售16元,第三车间继续加工加工费4元,然后售价24元。原料N的单位购入价为5元,每工时工资为15元,第一车间加工一个单位N,需要0.05工时,第二个0.1工时,第三个0.08工时,每个月最多得到12000个N,工时最多为1000工时。如何生产,收益最大?
问题分析
假设变量:
x1:产品A的售出量。
x2:产品A在第二车间加工后售出量.
x3:产品B售出量。
x4:产品B在第三车间加工后售出量。
x5:第一车间所用原材料数量。
- 第一车间所有原材料费和人工费为:5x5+0.05×15x5=5.75x5(下面计算盈利时,均已除去第一车间的材料和人工费)
-
A直接售出,盈利:10x1。
- A加工后售出,因为有额外加工费、人工费:5+0.1×15=6.5,售价-额外成本=19-6.5=12.5,盈利12.5x2。
- B直接售出,盈利16x3。
- B加工后售出,额外费用4+0.08×15=5.2,售价-成本=24-5.2=18.8,盈利18.8x4。
- 总盈利:z=10x1+12.5x2+16x3+18.8x4-5.75x5。
- 所以目标函数和约束条件如下:
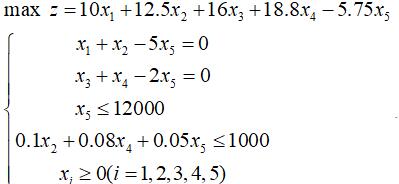
完美图解
转化为标准型,目标函数也重新表示:
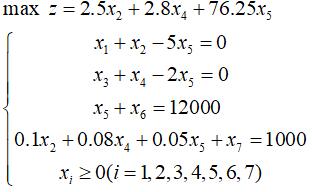
基本变量为:x1,x3,x6,x7。
非基本变量:x2,x4,x5。
建立单纯形表如下:
| b | x2 | x4 | x5 | |
|---|---|---|---|---|
| c | 0 | 2.5 | 2.8 | 76.25 |
| x1 | 0 | 1 | 0 | -5 |
| x3 | 0 | 0 | 1 | -2 |
| x6 | 12000 | 0 | 0 | 1 |
| x7 | 1000 | 0.1 | 0.08 | 0.05 |
具体图解过程不再重述。
代码实现
全局变量如下:
float kernel[100][100];//存储非单纯形表
char FJL[100] = {};//非基本变量
char JL[100] = {};//基本变量
int n, m, i, j;
代码内容如下:
void print()//输出单纯型表
{
cout<<endl;
cout<<"----------单纯形表如下:----------"<<endl;
cout<<" ";
cout<<setw(7)<<"b ";
for(i=1;i<=m;i++)
cout<<setw(7)<<"x"<<FJL[i];
cout<<endl;
cout<<"c ";
for(i=0;i<=n;i++)
{
if(i>=1)
cout<<"x"<<JL[i];
for(j=0;j<=m;j++)
cout<<setw(7)<<kernel[i][j]<<" ";
cout<<endl;
}
}
void DCXA()
{
float max1; //max1用于存放最大的检验数
float max2; //max2用于存放最大正检验数对应的基本变量的最大系数
int e=-1; //记录入基列
int k=-1; //记录离基行
float min;
//循环迭代,直到找到问题的解或无解为止
while(true)
{
max1=0;
min=100000000;
for(j=1;j<=m;j++) //找入基列(最大正检验数对应的列)
{
if(max1<kernel[0][j])
{
max1=kernel[0][j];
e=j;
}
}
if(max1<=0) //最大值小于等于0,即所有检验数小于等于0,满足获得最优解的条件
{
cout<<endl;
cout<<"获得最优解:"<<kernel[0][0]<< endl;
print();
break;
}
for(j=1;j<=m;j++) //判断正检验数对应的列是否都小于等于0,如果是则无界解
{
max2=0;
if(kernel[0][j]>0)
{
for(i=1;i<=n;i++) //搜索正检验数对应的列
if(max2<kernel[i][j])
max2=kernel[i][j];
if(max2==0)
{
cout<<"解无界"<<endl;
return;//退出函数,不能用break,因为它只是退出当前循环
}
}
}
for(i=1;i<=n;i++) //找离基行(常数列/入基列正比值最小对应的行)
{
float temp=kernel[i][0]/kernel[i][e]; //常数项在前,temp=fabs(temp);
if(temp>0&&temp<min) //找离基变量
{
min=temp;
k=i;
}
}
cout<<"入基变量:"<<"x"<<FJL[e]<<" ";
cout<<"离基变量:"<<"x"<<JL[k]<<endl;
//换基变换(转轴变换)
char temp=FJL[e];
FJL[e]=JL[k];
JL[k]=temp;
for(i=0;i<=n;i++) //计算除入基列和出基行的所有位置的元素
{
if(i!=k)
{
for(j=0;j<=m;j++)
{
if(j!=e)
{
if(i==0&&j==0) //计算特殊位c0,即目标函数的值
kernel[i][j]=kernel[i][j]+kernel[i][e]*kernel[k][j]/kernel[k][e];
else //一般位置
kernel[i][j]=kernel[i][j]-kernel[i][e]*kernel[k][j]/kernel[k][e];
}
}
}
}
for(i=0;i<=n;i++) //计算特殊位,入基列的元素
{
if(i!=k)
kernel[i][e]=-kernel[i][e]/kernel[k][e];
}
for(j=0;j<=m;j++) //计算特殊位,离基行的元素
{
if(j!=e)
kernel[k][j]=kernel[k][j]/kernel[k][e];
}
//计算特殊位,交叉位置
kernel[k][e]=1/kernel[k][e];
print();
}
}
复杂度分析
- 时间复杂度:在输入基本变量和非基本变量中用了n+m循环次数,在输入单纯形表时有nm此循环,打印最优解时有n+nm次的时间打印结果,在寻找入基列和离基行中,最坏情况下有O(n*m)次循环,在循环迭代中最坏情况需要2n迭代,则时间复杂度为O(2n)。
- 空间复杂度:O(1)。


文章评论