配对方案问题
问题分析
先了解几个概念。
二分图：又称二部图。设G=(V,E)是一个无向图，如果结点集V客分割为两个互不相交的子集（V1,V2），并且图中的每条边（i,j）所关联的两个结点i和j分别属于这两个不同的结点集（i∈V1，j∈V2），则称图G是一个二分图。
匹配：在图论中，一个匹配是一个边的集合，其中任意两条边都没有公共结点。
最大匹配：一个图所有匹配中，边数最多的匹配，成为这个图的最大匹配。
最佳推销员配对方案要求两个推销员男女搭配，相当于男女推销员形成了两个不相交的集合，可以配合工作的男女推销员有连线，求最大配对数，实际上这就是一个简单的二分图最大匹配问题。可以借助最大流算法，通过下面的变换，把二分图转化成网络，求最大流即可。
将二分图左边添加1个源点，右边添加一个汇点，将左边的点全部与源点相连，有边的点和汇点相连，所有边容量均为1.前面为女推销员编号，后面为男推销员编号，有连线表示两个人可以配合，男男之间、女女之间没有连线，构成网络。然后求网络最大流即可。
算法设计
- 构建网络：根据输入的数据，增加源点和汇点，每条边的容量设置为1，创建混合网络。
- 求网络最大流。
- 输出最大流值就是最大的配对数。
- 搜索女推销员结点的邻接表，流量为1的边对应的邻接点就是该女推销员的配对方案。
算法解释
如图1所示的关系。
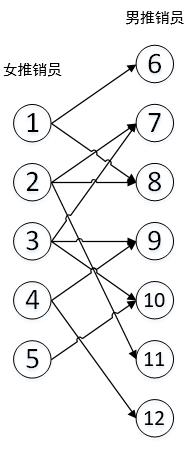
图1
- 构建网络。构建网络如图所示。
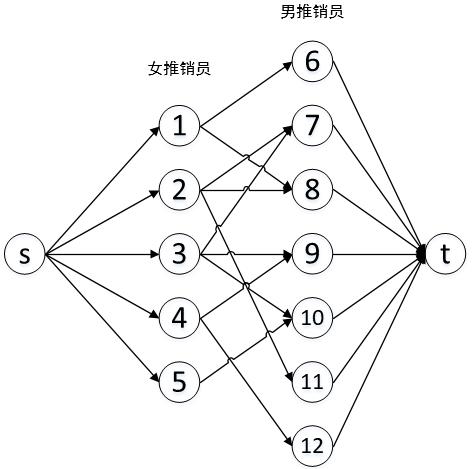
图2
- 求网络最大流。使用优化的ISAP算法求网络最大流，找到5条可增广路径。分别是：
- 13-10-5-0，增流：1。
- 13-9-4-0，增流：1。
- 13-7-3-0，增流：1。
- 13-11-2-0，增流：1。
- 13-8-1-0，增流：1。
增流后的实流网络如图3所示。
- 输出最大流值就是最多的配对数。搜索女推销员结点的邻接表，流量为1的边对应的邻接点就是该女推销员的配对方案。最大配对数5。配对方案：1-8,2-11,3-7,4-9，5-10。
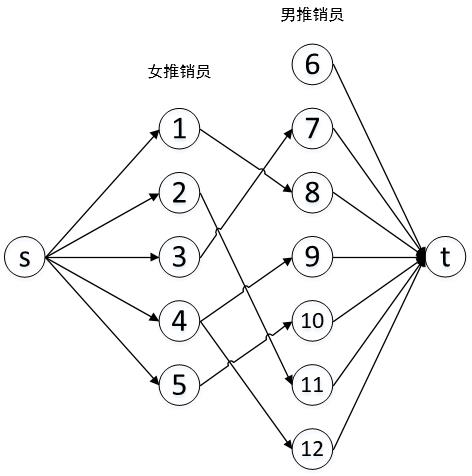
图3
代码实现
（1）创建混合网络邻接表
| 1 2 3 4 5 6 7 8 | for(int i=1;i<=m;i++) add(0, i, 1);//源点到女推销员的边 for(int j=m+1;j<=total;j++) add(j, total+1, 1);//男推销员到汇点的边 cout<<"请输入可以配合的女推销员编号u和男推销员编号v(两个都为-1结束):"<<endl; while(cin>>u>>v,u+v!=-2) add(u,v,1); |
（2） 求网络最大流。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | int Isap(int s, int t,int n) { set_h(t,n); int ans=0, u=s; int d; while(h[s]<n) { int i=V[u].first; if(u==s) d=inf; for(; ~i; i=E[i].next) { int v=E[i].v; if(E[i].cap>E[i].flow && h[u]==h[v]+1) { u=v; pre[v]=i; d=min(d, E[i].cap-E[i].flow); if(u==t) { cout<<endl; cout<<"增广路径："<<t; while(u!=s) { int j=pre[u]; E[j].flow+=d; E[j^1].flow-=d; u=E[j^1].v; cout<<"--"<<u; } cout<<"增流："<<d<<endl; ans+=d; d=inf; } break; } } if(i==-1) { if(--g[h[u]]==0) break; int hmin=n-1; //cur[u]=V[u].first; for(int j=V[u].first; ~j; j=E[j].next) if(E[j].cap>E[j].flow) hmin=min(hmin, h[E[j].v]); h[u]=hmin+1; cout<<"重贴标签后高度"<<endl; cout<<"h[ ]="; for(int i=1;i<=n;i++) cout<<" "<<h[i]; cout<<endl; ++g[h[u]]; if(u!=s) u=E[pre[u]^1].v; } } return ans; } |
（3）输出最佳配对数
| 1 2 3 | cout<<"最大配对数:"<<Isap(0,total+1,total+2)<<endl; cout<<endl; |
（4）输出最佳配对方案如下：
| 1 2 3 4 5 6 7 8 9 10 11 12 | void printflow(int n)//输出配对方案 { cout<<"----------配对方案如下：----------"<<endl; for(int i=1;i<=n;i++) for(int j=V[i].first;~j;j=E[j].next) if(E[j].flow>0) { cout<<i<<"--"<<E[j].v<<endl; break; } } |
算法复杂度分析
（1）时间复杂度：O(V2E)。
（2）空间复杂度：O(V)。
算法优化拓展——匈牙利算法
在匹配问题中，增广路经是指一条可以使匹配数变多的路径。
匈牙利算法的思想是不停地找增广路经，并增加匹配的个数，可以证明，当不能再找到增广路经时，就得到了一个最大匹配。
算法设计
- 根据输入的数据，创建邻接表。
- 初始化所有结点为未访问，检查第一个集合中的每一个结点u。
- 依次检查u的邻接点v。如果v未被访问，则标记已访问，然后判断如果v未匹配，则令u、v匹配，即match[u]=v,match[v]=u，返回true；如果v已匹配，则从v的邻接点出发，查找是否有增广路径，如果有则沿增广路径反色，然后令u、v匹配，即match[u]=v,match[v]=u，返回true。否则返回false，转第2步。
- 当找不到增广路径的时候，即得到一个最大匹配。
完美图解
- 根据输入的数据，创建邻接表。
- 初始化访问数组vis[i]=0,i=1,2,3,...,12。检查1的第一个邻接点6,6未被访问，标记vis[6]=1.6未匹配，则令1和6匹配，即match[6]=1,match[1]=6,return true。
- 初始化访问数组vis[i]=0；检查2的第一个邻接点7，7未被访问，标记vis[7]=1。7未匹配，则令2和7匹配，即match[7]=2，match[2]=7,return true。
- 初始化访问数组vis[i]=0；检查3的第一个邻接点7，7未被访问，标记vis[7]=1。7已匹配，match[7]=2，即7的匹配点为2，从2出发寻找增广路径。实际上这就是为2再找一个匹配点，如果找到了，就把之前匹配的那个点让给3号，如果2没有找到，那么就拒绝3的请求，让3继续往下找。从2出发，检查2的第一个邻接点7,7已访问，然后检查第二个邻接点8,8未访问，标记vis[8]=1。8未匹配，则令2和8匹配，即match[8]=2，match[2]=8，返回true。2号找到一个结点之后就把原来的匹配点7让给了3，令match[3]=7，match[7]=3，返回true。
- 初始化访问数组vis[i]=0；检查4的第一个邻接点9，9未被访问，标记vis[9]=1。9未匹配，则令4和9匹配，即match[4]=9，match[9]=4,return true。
- 初始化访问数组vis[i]=0；检查5的第一个邻接点10，10未被访问，标记vis[10]=1。10未匹配，则令5和10匹配，即match[5]=10，match[10]=5,return true。
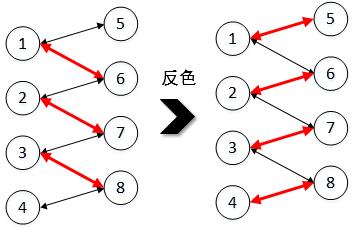
反色过程：检查4号的邻接点8，发现8已匹配，match[8]=3，从3出发，检查3号的邻接点7，发现7已经匹配，match[7]=2，检查2号的邻接点6，发现6已经匹配，match[6]=1，检查1号的邻接点5，发现5未匹配，找到一条增广路经：3-7-2-6-1-5，立即反色。令match[5]=1,1h奥找到了匹配点就把原来的匹配点6让给了2号，match[2]=6；2号找到了匹配点就立即把原来的匹配点7让给了3号，match[3]=7；3号找到了匹配点就立即把8号让给了4号，match[4]=8。
复杂度分析
时间复杂度：找到一条增广路经的复杂度最坏为O(E)，最多有V条增广路，所以时间复杂度O(VE)，与最大网络流算法的时间复杂度O(V2E)相比下降不少。
圆桌问题
X集合中的点到Y集合中的每个点都有连线，所有连线容量都是1，保证两个点只能匹配一次（一个餐桌上只能有同一个单位的一个人）。这种在一个二分图中每个结点可以有多个匹配结点的问题称为二分图多重匹配问题。求解时需要添加源点和汇点，源和汇的边容量分别限制X、Y集合中每一个点匹配的个数。
简历一个二分图，每个代表团为X集合中的结点，每个会议桌为Y集合中的结点，增设源点s和汇点t。从源点s向每个xi结点链接一条容量为该店标团人数ri的有向边，从每个yi结点向汇点t链接一条容量为该会议桌容量cj的有向边。X集合中每个结点向Y集合中每个结点链接一条容量为1的有向边。
算法设计
- 构建网络。根据输入的数据，建立二分图，每个代表团为X集合中的结点，每个会议桌为Y集合中的结点，增设源点s和汇点t。从源点s向每个xi结点链接一条容量为该店标团人数ri的有向边，从每个yi结点向汇点t链接一条容量为该会议桌容量cj的有向边。X集合中每个结点向Y集合中每个结点链接一条容量为1的有向边。创建混合网络。
- 求网络最大流。
- 输出安排方案。如果最大流值等于源点s与X集合所有结点边容量之和，则说明X集合每个结点都有完备的多重匹配，否则无解。对于每个代表团来说，从X集合对应点出发的所有流量为1的边指向的Y集合的结点就是该代表团人员的安排情况（一个可行解）。
完美图解
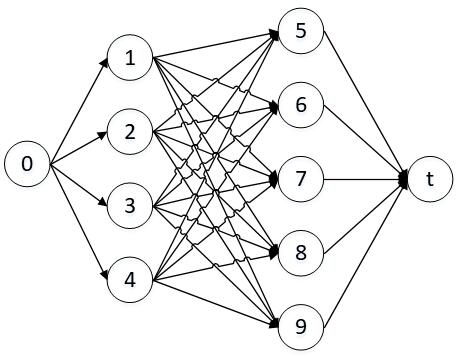
假设代表团数M=4，每个代表团人数依次为2、4、3、5；会议桌数n=5，每个会议桌可安排人数依次为3、4、2、5、4.
- 构建网络。
- 求最大网络流。使用ISAP算法求网络最大流，找到14条增广路径。
- 增广路经：10-9-4-0。增流1。
- 增广路经：10-8-4-0。增流1。
- 增广路经：10-7-4-0。增流1。
- 增广路经：10-6-4-0。增流1。
- 增广路经：10-5-4-0。增流1。
- 增广路经：10-9-3-0。增流1。
- 增广路经：10-8-3-0。增流1。
- 增广路经：10-7-3-0。增流1。
- 增广路经：10-9-2-0。增流1。
- 增广路经：10-8-2-0。增流1。
- 增广路经：10-6-2-0。增流1。
- 增广路经：10-5-2-0。增流1。
- 增广路经：10-9-1-0。增流1。
- 增广路经：10-8-1-0。增流1。
增流后的实流网络如下图所示。
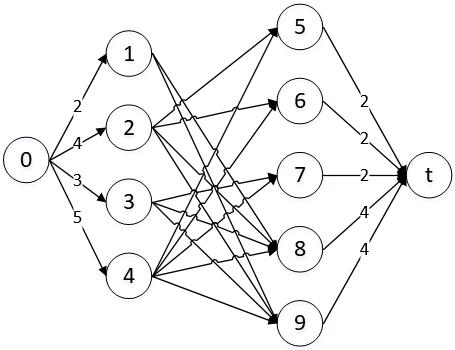
- 输出安排方案。最大流值等于源点s与X几何所有结点边容量之和14，说明每个代表团都有完备的多重匹配。对于每个代表团，从代表团结点出发的所有流量为1的边指向的结点就是该代表团人员的会议桌号。在程序中，会议桌储存编号=代表团数m+实际编号，输出时需要输出会议桌实际编号。
代码实现
（1）构建混合网络。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | cout<<"请输入代表团数m和会议桌数n:"<<endl; cin>>m>>n; init(); total=m+n; cout<<"请依次输入每个代表团人数:"<<endl; for(int i=1;i<=m;i++) { cin>>cost; sum+=cost; add(0, i, cost);//源点到代表团的边，容量为该代表团人数 } cout<<"请依次输入每个会议桌可安排人数:"<<endl; for(int j=m+1;j<=total;j++) { cin>>cost; add(j, total+1, cost);//会议桌到汇点的边，容量为会议桌可安排人数 } for(int i=1;i<=m;i++) for(int j=m+1;j<=total;j++) add(i, j, 1);//代表团到会议桌的边，容量为1 |
（3）输出安排方案
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | if(sum==Isap(0,total+1,total+2)) { cout<<"会议桌安排成功！"; cout<<endl; print(m,n);//输出最佳方案 cout<<endl; printg(total+2);//输出最终网络邻接表 } else cout<<"无法安排所有代表团！"; void print(int m,int n)//输出安排方案 { cout<<"----------安排方案如下：----------"<<endl; cout<<"每个代表团的安排情况："<<endl; for(int i=1;i<=m;i++)//读每个代表团的邻接表 { cout<<"第"<<i<<"个代表团安排的会议桌号:"; for(int j=V[i].first;~j;j=E[j].next)//读第i个代表团的邻接表 if(E[j].flow==1) cout<<E[j].v-m<<" "; cout<<endl; } } |
算法复杂度
时间复杂度：找到一条可增广路时间为O(V)，最多会执行O(VE)次，因为关键边的总数为O(VE)，因此总的时间复杂度为O(V2E)，其中V为结点个数，E为边的数量。
空间复杂度O(V)。
试题库问题
这仍然是一个二分图多重分配问题。
算法设计
- 构建网络。根据输入的数据，简历二分图，每个题型为X集合中的结点，每个实体为Y集合中的结点，增设源点s和汇点t。从源点s向每个xi有一条有向边，容量为该题型选出的数量ci。从每个yi向t连接一条有向边，容量为1，以保障每道题只能选中一次。Y集合中的题属于哪些题型，则xi就和yi之间有一条有向边，容量为1，创建混合网络。
- 求网络最大流。
- 输出抽取方案。如果最大流值等于源点s与X集合所有结点边容量之和，则说明实体抽取成功，否则无解。对于每个题型来说，从X集合对应点出发的所有流量为1的边指向的Y集合的结点就是该题型选中的试题号（一个可行解）。
完美图解
假设题型数m=4，实体总数n=15，我们要在每种题型依次选择2、0、3、2个实体。上述的15个实体中，每个实体所属的题型依次是：1/2；2/3；1/4；2/3；2/4；1/2/3；3；4；4；2/3/4；3；2；1；1、4；4。
- 构建网络。
- 使用ISAP算法求网络最大流，找到7条增广路径。
- 增广路经：20-19-4-0。增流：1。
- 增广路经：20-18-4-0。增流：1。
- 增广路经：20-15-3-0。增流：1。
- 增广路经：20-14-3-0。增流：1。
- 增广路经：20-11-3-0。增流：1。
- 增广路经：20-17-1-0。增流：1。
- 增广路经：20-10-1-0。增流：1。
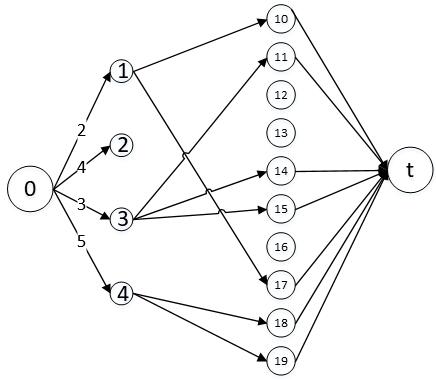
- 输出抽取方案。最大流值等于抽取的试题数之和，说明试题抽取成功。
算法复杂度
时间复杂度：找到一条可增广路时间为O(V)，最多会执行O(VE)次，因为关键边的总数为O(VE)，因此总的时间复杂度为O(V2E)，其中V为结点个数，E为边的数量。
空间复杂度O(V)。
