参考视频:https://space.bilibili.com/230105574/
阅读原文请访问:https://qouwscohey.feishu.cn/docs/doccnAtfHvdvbQZzj5YfXWX8Etd
第一节:递归算法
不确定性:①不存在完美的数学模型;②系统的扰动不可控,也很难建模;③测量传感器存在误差。
我们可以发现,随着k增大,1/k趋近于0,那么xk->xk-1。也就是说,随着k增加,测量结果不再重要。而k越小,1/k越大,zk的作用越大。
如果我们把1/k用一个参数Kk来代替,则公式可以调整为
$$\hat{X}_k=\hat{X}_{k-1}+K_k(z_k-\hat{X}_{k-1})$$
也就是说,当前的估计值=上一次的估计值+系数×(当前测量值-上一次的估计值)
其中这个系数就是Kalman Gain,也就是卡尔曼增益。
我们定义这样一些参数:
- 估计误差e_est:估计值与真实值之间的误差。
- 测量误差e_MEA:测量值与真实值之间的误差。
那么,
$$K_k=\frac{e_{ESTk-1}}{e_{ESTk-1}+e_{MEAk}}$$
这是卡尔曼滤波器的核心公式。
讨论:在k时刻:
①e_estk-1>>e_MEAk,则K_k->1,则X_k=z_k。也就是说,当k-1时的估计误差远远大于k时的测量误差,那么低k次的估计值就为第k次的测量值了。这也是符合预期的,因为估计误差越大,说明第k-1次的估计值越不可信,那么就只能用当前计算值作为估计值了。
②e_estk-1<<e_MEAk,则K_k->0,则X_k=X_{k-1}。也就是说,当k-1的估计误差远远小于测量误差,也就是测量值越不可信的时候,那么只能用前一次估计值作为当前估计值了。
kalman滤波器可以分为三步:
Step 1:计算kalman gain:$$K_k=\frac{e_{ESTk-1}}{e_{ESTk-1}+e_{MEAk}}$$
Step 2:计算$$\hat{X}_k=\hat{X}_{k-1}+K_k(z_k-\hat{X}_{k-1})$$
Step 3:更新$$e_{ESTk}=(1-K_k)e_{ESTk-1}$$
其实所谓的新息就是$$z_k-\hat{X}_{k-1}$$,即系统测量的第k次真实值-上一次估计值。
数据融合(Data Fusion)
假设我们测量一个东西,第一次测量出来的结果z1=30g,第二次测量出来的结果z2=32g,他们的标准差分别为2和4,且服从正态分布。那么对于第一次测量来说,它有68.4%的概率为28~32g之间;而对于第一次测量来说,他有68.4%的概率分布在28g~36g。
现在我们有了以上两个结果,该怎样估计真实值呢?
可以使用上一节中提到的kalman的迭代公式的思想来解决这个问题。即可以用$$\hat{Z}=\hat{Z}_{1}+K_k(z_2-\hat{X}_{1})$$的思想来解决这个问题。即问题的求解目标是:求解一个K,使得$$\sigma_{\hat{Z}}$$最小,也就是使得方差var($$\hat{z}$$)最小。推导公式如下:
这个过程就叫做数据融合。
将方差和协方差放到一个矩阵里面,体现了变量间的联动关系。
那么协方差矩阵反映了什么?它反映了两类数据(方差是同类数据)之间的关系,若方差越大,说明数据波动越大,没太有明显规律。若协方差正向越大,说明两类数据越相关,越小反映越不相关,为负说明他们负相关。
连续系统的状态空间表达式状态方程是由控制系统的状态变量和控制变量构成的一阶微分方程组。 输出方程是该系统输出变量与状态变量和控制变量的函数关系式。
$$X_{k}=AX_{k-1}+Bu_{k}$$
$$Z_k=HX_k$$
在实际使用中,可以对两个公式分别加上两个参数,变为
$$X_{k}=AX_{k-1}+Bu_{k-1}+\omega_{k-1}$$状态方程,Xk是状态变量,A是状态矩阵,B是控制矩阵,uk-1是控制量。
$$Z_k=HX_k+\nu_{k}$$测量状态方程
其中$$\omega_{k-1}$$被称为过程噪声(Process Noise),$$\nu_{k}$$被称为测量噪声(Measure Noise)。
卡尔曼滤波器要解决的问题就是如何估计一个更精确的$$\hat{X}_{k}$$。我们有一个不太准确的计算值和不太准确的测量值,通过“数据融合”找到一个比他们误差都要小的值。
在上一节中,我们已经得到了两个状态方程:
$$X_{k}=AX_{k-1}+Bu_{k-1}+\omega_{k-1}$$和$$Z_k=HX_k+\nu_{k}$$。其中$$\omega_{k-1}$$服从于期望为0,协方差矩阵为Q的正态分布($$Q=E[\omega\omega^T]$$);$$\nu_{k}$$服从于期望为0,协方差矩阵R的正态分布($$R=E[vv^T]$$)。
在这两个公式中,我们不知道这两个噪声,但是我们可以计算出来
$$\hat{X_k^-}=A\hat{X_{k-1}}+Bu_{k-1}$$①
$$Z_{k}=HX_{k}--->\hat{X_{kmea}}=H^-Z_k$$②
其中$$\hat{X_k^-}$$代表$$X_k$$的先验估计值(即直接通过状态方程计算出来的,不包括噪声);$$\hat{X_{kmea}}$$代表测量值。①为计算出来的式子,②为测量出来的。
那么根据第二节中的数据融合的公式$$\hat{Z}=\hat{Z}_{1}+K_k(z_2-\hat{X}_{1})$$可以得到
$$\hat{X_k}=\hat{X_k^-}+G(H^-Z_k-\hat{X_k^-})$$
可以看出,当G=0的时候,$$\hat{X_k}=\hat{X_k^-}$$;当G=1的时候,$$\hat{X_k}=H^-Z_k$$。在很多教科书上,会做一个这样的处理:令$$G=K_kH$$,则:
$$\hat{X_k}=\hat{X_k^-}+K_k(Z_k-H\hat{X_k^-})$$这是一个非常关键的式子
这个时候$$K_k\in[0,H^-]$$
所以,又回到第二节的基础,我们的目标就是寻求一个$$K_k$$使得$$\hat{X_k}\to X_k$$。
怎样让两个值更接近呢?其实我们想当然就会想到考虑计算误差和测量误差。如果计算误差较大,我们可能更倾向于选择测量值;如果测量误差较大,我们更倾向于选择计算值。所以Kk的取值和误差息息相关。
为了衡量这个问题,我们引入$$e_k=X_k-\hat{X_k}$$,同时,$$p(e_k) \to (0,P)$$,且$$P=E[ee^T]=\begin{bmatrix} \sigma_{e_1}^2 & \sigma_{e_1}\sigma_{e_2} \\ \sigma_{e_2}\sigma_{e_1} & \sigma{e_2}^2 \end{bmatrix}$$。
如果说Xk距离实际值越小,说明误差的方差最小,方差最小说明期望越接近于0。我们希望选取合适的$$K_k$$,使得tr(P)越小。$$tr(P)=\sigma_{e_1}^2 +\sigma_{e_2}^2 $$。
我们令$$e_k=X_k-\hat{X_k}$$。那么,
$$P=E[ee^T]=E[(X_k-\hat{X_k})(X_k-\hat{X_k})^T]$$③
单独来看$$X_k-\hat{X_k}$$,它可以展开为
$$X_k-\hat{X_k}=X_k-(\hat{X_k^-}+K_k(Z_k-H\hat{X_k^-})=X_k-\hat{X_k^-}-K_kZ_k+K_kH\hat{X_k^-}$$
将$$Z_k=HX_k+\nu_{k}$$带入上式可得
$$X_k-\hat{X_k^-}-K_kHX_k-K_kv_k+K_kH\hat{X_k^-}=(X_k-\hat{X_k^-})-K_kH(X_k-\hat{X_k^-})-K_kv_k$$
$$=(I-K_kH)(X_k-\hat{X_k^-})-K_kv_k=(I-K_kH)e_k^--K_kv_k$$④
其中先验误差$$e_k^-=X_k-\hat{X_k^-}$$
将④带入③可以得到
$$E[[(I-K_kH)e_k^- -K_kv_k][(I-K_kH)e_k^- -K_kv_k]^T]$$$$=E[(I-K_kH)e_k^- e_k^{-T} (I-K_kH)^T-(I-K_kH)e_k^-v_k^TK_k^T-K_kv_ke_k^{-T}(I-K_kH)^T+K_kv_kv_k^TK_k^T]$$$$=E[(I-K_kH)e_k^- e_k^- (I-K_kH)^T]-E[(I-K_kH)e_k^-v_k^TK_k^T-K_kv_ke_k^{-T}(I-K_kH)^T]$$
$$+E[K_kv_kv_k^TK_k^T]$$$$
$$=E[(I-K_kH)e_k^- e_k^{-T} (I-K_kH)^T]-(I-K_kH)E[e_k^-v_k^T]K_k^T-K_kE[v_ke_k^{-T}](I-K_kH)^T]$$
$$+E[K_kv_kv_k^TK_k^T$$
注意,上式中e的上标-T中,-指的是先验的意思,T是转置。
因为先验误差$$e_k^-$$和测量噪声$$v_k^T$$相互独立,先验误差只和过程噪声有关系,所以$$E[e_k^-v_k^T]=E[e_k^-]E[v_k^T]=0$$,所以上式中的第二项和第三项为0。也就变成了$$(I-K_kH)E[e_k^- e_k^{-T}] (I-K_kH)^T+K_kE[v_kv_k^T]K_k^T$$⑤
类比③式可以得到
$$(I-K_kH)P_k^- (I-K_kH)^T+K_kE[v_kv_k^T]K_k^T$$⑥
其中$$P_k^-$$是先验误差的协方差矩阵。由第三节的第三行可以知道$$R=E[vv^T]$$,所以上式可以表示为
$$(P_k^- -K_kHP_k^-)(I-H^TK_kT)+K_kRK_k^T$$
$$=P_k^- -K_kHP_k^- -P_k^-H^TK_k^T +K_kHP_k^-H^TK_k^T+K_kRK_k^T$$⑦
由③④⑤⑥⑦可得
$$P_k=P_k^- -K_kHP_k^- -P_k^-H^TK_k^T +K_kHP_k^-H^TK_k^T+K_kRK_k^T$$⑧
前面我们说了,我们要选取合适的$$K_k$$,使得tr(P)越小。
我们先来看第三项$$P_k^-H^TK_k^T $$,对他求转置可以得到$$[(P_k^-H^T)K_k^T]^T=K_kHP_k^-$$
看来第三项是第二项的转置。由于互为转置的两个矩阵迹一样(因为对角线元素一样)
所以对⑧求迹可以得到
$$tr(P_k)=tr(P_k^-)-2tr(K_kHP_k^-)+tr(K_kHP_k^-H^TK_k^T)+tr(K_kRK_k^T)$$⑨
寻找$$K_k$$使得这个迹最小,则对$$tr(P_k)$$求导
$$\frac{\partial tr(P_k)}{\partial A}=0-2(HP_k^-)^T+2K_kHP_k^-H^T+2K_kR=0$$⑩
$$\frac{\partial tr(AB)}{\partial A}=B^T$$举例,假如$$A=\begin{bmatrix} a_{11} & a_{12} \\a_{21} & a_{22}\end{bmatrix}$$,$$B=\begin{bmatrix} b_{11} & b_{12} \\b_{21} & b_{22}\end{bmatrix}$$,那么$$tr(AB)=a_{11}b_{11}+a_{12}b_{21}+a_{21}b_{12}+a_{22}b_{22}$$则将上式对A求偏导可得:$$\frac{\partial tr(AB)}{\partial A}=\begin{bmatrix} \frac{\partial tr(AB)}{\partial a_{11}} & \frac{\partial tr(AB)}{\partial a_{11}} \\\frac{\partial tr(AB)}{\partial a_{21}} & \frac{\partial tr(AB)}{\partial a_{22}}\end{bmatrix}=\begin{bmatrix} b_{11} & b_{21} \\b_{12} & b_{22}\end{bmatrix}=B^T$$故可以求解出⑨式的第二项再看第三项和第四项,相当于$$\frac{\partial tr(ABA^T)}{\partial A}=2AB$$
由⑩式可以得到$$P_k^{-T}H^T-K_kHP_k^-H^T-K_kR=0$$
所以
$$P_k^-H^T+K_k(HP_k^-H^T+R)=0$$
所以$$K_k(HP_K^-H^T+R)=P_k^-H^T$$
所以$$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$$
上式就是卡尔曼滤波器里面最重要的公式,即Kalman Gain。
可以分析到,当R特别大(R是测量噪声矩阵协方差),Kk->0,更偏向于信任上一次估计值。当R特别小的时候,$$K_k=\frac{P_k^-H^T}{HP_k^-H^T}=H^-$$,$$\hat{X_k}=H^-Z_k$$。
总结一下上一节的几个公式:
$$X_k=AX_{k-1}+Bu_{k-1}+\omega_{k-1}$$①
$$Z_k=HX_k+v_{k-1}$$②
先验估计为
$$\hat{X_k^-}=A\hat{X_{k-1}} + Bu_{k-1}$$③
后验估计为
$$\hat{X_k}=\hat{X_{k-1}^-} + K_k(Z_k-H\hat{X_k^-})$$④
其中卡尔曼增益$$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$$⑤
我们发现在上面③④⑤式中,除了协方差矩阵$$P_k^-$$,我们都已经知道。其中$$u_{k-1}$$是输入。
我们知道$$e_k^-=X_k-\hat{X_k^-}$$,将式①和式③带入可以得到
$$e_k^-=AX_{k-1}+Bu_{k-1}+\omega_{k-1}-A\hat{X_{k-1}} -Bu_{k-1}=A(X_{k-1}-\hat{X_{k-1}})+\omega_{k-1}$$
因为$$(X_{k-1}-\hat{X_{k-1}})=e_{k-1}$$
所以$$P_k^-=E[e_k^-e_k^{-T}]=E[(Ae_{k-1}+\omega_{k-1})(Ae_{k-1}+\omega_{k-1})^T]=E[(Ae_{k-1}+\omega_{k-1})(e_{k-1}^TA^T+\omega_{k-1}^T)]$$
将上式展开并进行组合可以得到
$$E[Ae_{k-1}e_{k-1}^TA^T]+E[Ae_{k-1}\omega_{k-1}]+E[\omega_{k-1}e_{k-1}^TA^T]+E[\omega_{k-1}\omega_{k-1}^T]$$④
$$e_{k-1}$$和$$\omega_{k-1}$$相互独立。这是为什么呢?因为$$\omega_{k-1}$$作用于$$X_k$$,而$$e_{k-1}=X_{k-1}-\hat{X_{k-1}}$$,所以他们是相互独立的。
因为$$e_{k-1}$$和$$\omega_{k-1}$$相互独立,所以④式中第二项和第三项为0,故④式可以进一步化简为
$$P_k^-=AP_{k-1}A^T+Q$$,其中Q是$$\omega$$的协方差矩阵。
至此推导结束。
那么总的来说,卡尔曼滤波器分为预测和校正两个步骤。
|
预测
|
校正
|
|
Step 1:求解先验:
$$\hat{X_k^-}=A\hat{X_{k-1}} + Bu_{k-1}$$
Step 2:求解先验误差协方差矩阵
$$P_k^-=AP_{k-1}A^T+Q$$
|
Step 3:计算卡尔曼增益
$$K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$$
Step 4:求解后验估计:
$$\hat{X_k}=\hat{X_{k-1}^-} + K_k(Z_k-H\hat{X_k^-})$$
Step 5:更新误差协方差矩阵
把Step3的公式带入第三节的式⑧
$$P_k=P_k^- -K_kHP_k^-=(I-K_kH)P_k^-$$
|
以上就是卡尔曼滤波器的五个公式了。对于第0次的时候,我们需要赋予初值$$\hat{X_{k-1}}$$和$$P_0$$。
例子:假如一个人在走路,设变量$$x_1$$代表其位置,变量$$x_2$$代表其速度。假如其为匀速走动,且采样间隔为$$\Delta T$$,那么位置和速度分别为
$$X_{1,k}=X_{1,k-1}+\Delta TX_{2,k-1}+\omega_{1,k-1}$$
$$X_{2,k}=X_{2,k}+\omega_{2,k-1}$$
其中$$\omega_1$$和$$\omega_2$$为过程噪声,均服从期望为0,协方差矩阵为Q的正态分布。这里我们领$$\Delta T$$=1。
假设有一个卫星来监测这个人的位置和速度,因为可能存在各种各样的误差,所以测量出来的位置和速度分别为
$$Z_{1,k}= X_{1,k}+v_{1,k}$$
$$Z_{2,k}=X_{2,k}+v_{2,k}$$
其中$$P(v)\backsim N(0,R)$$
那么,
$$\begin{bmatrix} X_{1,k} \\ X_{2,k} \end{bmatrix}=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} X_{1,k-1} \\ X_{2,k-1} \end{bmatrix}+\begin{bmatrix} \omega_{1,k-1} \\ \omega_{2,k-1} \end{bmatrix}$$
$$\begin{bmatrix} Z_{1,k} \\ Z_{2,k} \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} X_{1,k-1} \\ X_{2,k-1} \end{bmatrix}+\begin{bmatrix} v_{1,k-1} \\ v_{2,k-1} \end{bmatrix}$$
可以看出,上式就可以总结为两个二维的状态方程:
$$X_k = A X_{k-1}+\omega_{k-1}$$
$$Z_k=HZ_{k-1}+v_{k-1}$$
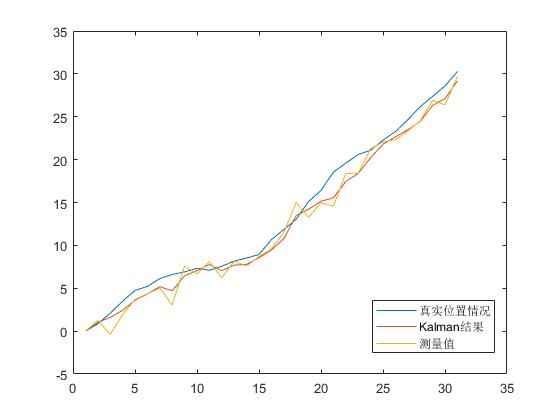
用两个不太准确的值估计出来的$$\hat{X_{k}}$$是最优的。
运行一次的结果,由于真实值和测量值是加了随机噪声,故每一次运行结果可能不一致。
阅读原文请访问:https://qouwscohey.feishu.cn/docs/doccnAtfHvdvbQZzj5YfXWX8Etd





文章评论