Leetcode 4：寻找两个有序数组的中位数

题目描述

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

解题思路

详见：
https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/4-xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-shu/

代码实现

 double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int n = nums1.size();
    int m = nums2.size();
    if (n > m)  //保证数组1一定最短
    {
        return findMedianSortedArrays(nums2, nums1);
    }
    // Ci 为第i个数组的割,比如C1为2时表示第1个数组只有2个元素。LMaxi为第i个数组割后的左元素。RMini为第i个数组割后的右元素。
    int LMax1, LMax2, RMin1, RMin2, c1, c2, lo = 0, hi = 2 * n;  //我们目前是虚拟加了'#'所以数组1是2*n长度
    while (lo <= hi)   //二分
    {
        c1 = (lo + hi) / 2;  //c1是二分的结果
        c2 = m + n - c1;
        LMax1 = (c1 == 0) ? INT_MIN : nums1[(c1 - 1) / 2];
        RMin1 = (c1 == 2 * n) ? INT_MAX : nums1[c1 / 2];
        LMax2 = (c2 == 0) ? INT_MIN : nums2[(c2 - 1) / 2];
        RMin2 = (c2 == 2 * m) ? INT_MAX : nums2[c2 / 2];
        if (LMax1 > RMin2)
            hi = c1 - 1;
        else if (LMax2 > RMin1)
            lo = c1 + 1;
        else
            break;
    }
    return (max(LMax1, LMax2) + min(RMin1, RMin2)) / 2.0;
    }

复杂度

Leetcode 5：最长回文子串

题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

输入: "cbbd"
输出: "bb"

解题思路

我们观察到回文中心的两侧互为镜像。因此，回文可以从它的中心展开，并且只有2n-1个这样的中心。

你可能会问，为什么会是2n-1个，而不是n个中心？原因在于所含字母数为偶数的回文的中心可以处于两字母之间。

参考：
https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode/

代码实现

int expend(string s, int left, int right)
{//以left和right为中心的回文串长度
    int L = left, R = right;
    while (L >= 0 && R < s.size() && s[R] == s[L])
    {
        L--;
        R++;
    }
    return R - L - 1;
}
string longestPalindrome(string s) {
    int len = s.size();
    if (len == 0 || len == 1)
        return s;
    int start = 0, end = 0, maxlen = 0;
    for (int i = 0; i < len;i++)
    {
        int len1 = expend(s, i, i);//一个元素为中心
        int len2 = expend(s, i, i + 1);//两个元素为中心
        maxlen = max(max(len1, len2), maxlen);
        if (maxlen > end - start + 1)
        {
            start = i - (maxlen - 1) / 2;
            end = i + maxlen/2;
        }
    }
    return s.substr(start, maxlen);
}

复杂度

时间复杂度：O(n^2)，由于围绕中心来扩展回文会耗去O(n)的时间，所以总的复杂度为 O(n^2)。
空间复杂度：O(1)。

Leetcode 48： 旋转图像

题目描述

给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

题目解析

旋转90°，可以当做两步：第一步是关于对角线取对称；第二步是关于水平线取上下对称。
记住这个原理。

代码实现

    void rotate(vector<vector<int> > &matrix) {
        //对角线对称
        int n=matrix.size();
        for(int i=0;i<n;i++)
            for(int j=0;j<n-i;j++)
                swap(matrix[i][j],matrix[n-1-j][n-1-i]);
        //上下交换
        for(int i=0;i<n/2;i++)
            for(int j=0;j<n;j++)
                swap(matrix[i][j],matrix[n-1-i][j]);

    }

复杂度

时间复杂度：O(n^2)

Leetcode 62：不同路径

题目描述

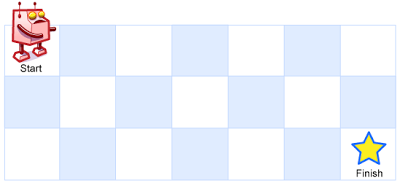
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

解题思路1：二维动态规划

我们通过思考画图可以发现，第一行第一列都只有1种路径，而对于其它位置来说，到达它的方法数等于到达它上面一个方格的方法数+到达它左侧一个方格的方法数。故可以写出：

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

代码实现1：二维动态规划

int uniquePaths(int m, int n) {
    vector < vector<int>>dp(n, vector<int>(m, 1));
    for (int i = 1; i < n; i++)
    {
        for (int j = 1; j < m; j++)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
    return dp[n - 1][m - 1];
}

复杂度1：二维动态规划

时间复杂度：O(m * n)，空间复杂度：O(m * n)。

代码实现2：一维动态规划

int uniquePaths(int m, int n) {
        vector<int>dp(n,1);
        for(int i=1;i<m;i++)
        {
            dp[0]=1;
            for(int j=1;j<n;j++){
                dp[j]=dp[j]+dp[j-1];
            }
        }
        return dp[n-1];
    }

复杂度2：一维动态规划

时间复杂度仍为O(m * n)，空间复杂度为O(n)。

Leetcode 64：最小路径和

题目描述

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。说明：每次只能向下或者向右移动一步。

示例

输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

解题思路

此题其实是62题的一个提升版本，也可以说62题是64题的一个特例，即是64题各格子上的数字为1的情况。

所以同样，对于第一列来说，每一个格子的数字总和的最小值（其实也就这一个值）为该列上一个格子的数字和加上当前格子上的数字；对于第一行来说，每一个格子的数字总和为该行上一个格子的数字和加上当前格子上的数字。

对于其它格子上来说，该格子上的数字总和=该格子上的数字+截止到前一步的和。由于该格子上的数字不能改变，所以只需要令前一步的和最小即可，也即

dp[i][j] += min(dp[i - 1][j], dp[i][j - 1]);

对于此题来说，由于可以直接在原矩阵上更新，所以没必要新建一个一维空间。

代码实现

int minPathSum(vector<vector<int>>& grid) {
    //直接在原矩阵操作
    int row = grid.size();//行数
    int col = grid[0].size();//列数
    //第一列更新
    for (int i = 1; i < row; i++)
    {
        grid[i][0] += grid[i - 1][0];
    }
    //第一行更新
    for (int i = 1; i < col; i++)
    {
        grid[0][i] += grid[0][i - 1];
    }
    //剩余行列更新
    for (int i = 1; i < row; i++)
    {
        for (int j = 1; j < col; j++)
        {
            grid[i][j] += min(grid[i - 1][j], grid[i][j - 1]);
        }
    }
    return grid[row-1][col-1];
}

复杂度分析

时间复杂度：O(m * n)，空间复杂度：不占用额外空间