Leetcode 148：排序链表

题目描述

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例

示例 1:
输入: 4->2->1->3
输出: 1->2->3->4

示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5

解题思路

由于题目要求复杂度为O(nlogn)且空间复杂度为常数级，我们可以想到的是堆排序，但是实际上，由于是链表，其不需要借助额外的数组来存储内容，只需要通过链表直接的链接调整即可，所以对于链表来说，归并排序的空间复杂度也是O(1)。当然在使用递归的时候就不是了。

归并排序的顺序是“二分”和“合并”。那么对于链表来说，由于我们不能使用递归，所以我们可以使用迭代来进行处理。首先是二分的步骤，其过程如下图所示。

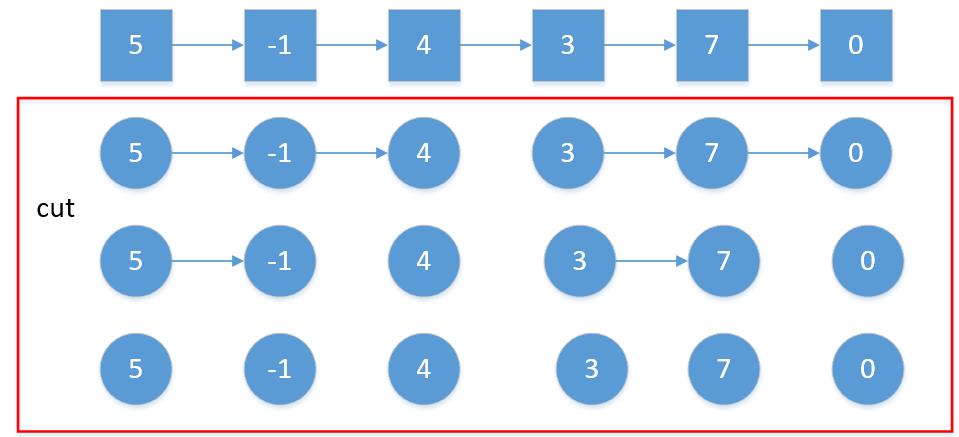
对于cut这个过程，我们要做的就是，首先记录下链表的长度n，其实每一次划分，其划分出来的长度都是n>>2，也就是二分之n，所以我们只需要将一个指针从头走n/2次即可，然后将该指针的next指向空，记录下一个节点的地址为right，并返回。这样我们就记录了两个子链表的开始地址left和right，如下图所示。

代码实现如下的cut函数所示。

在cut完成之后，就需要开始“合并”。合并这个工序可以参见之前做过的合并有序链表即可，其过程不再重述，如下图所示。

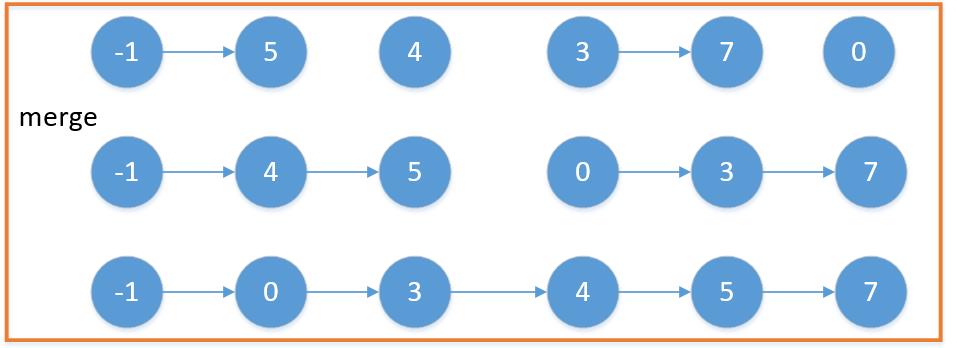
整个过程如下图所示。

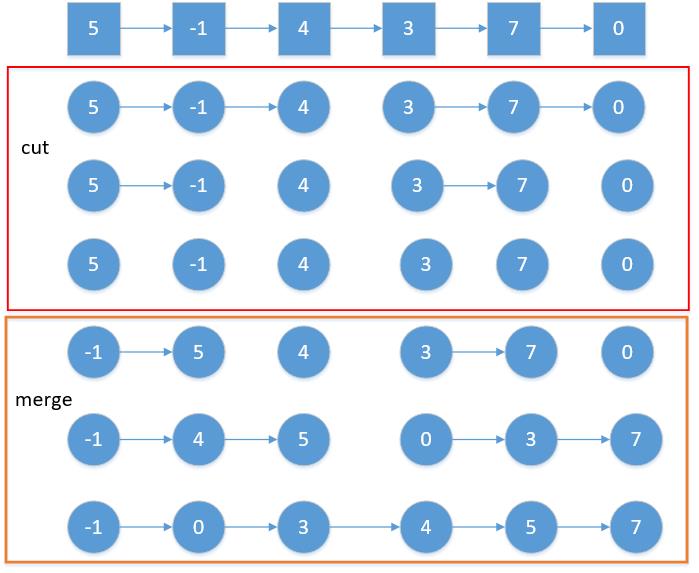
代码实现

class Solution {
public:
    ListNode* cut(ListNode* head, int n)
{
    auto p = head;
    while (--n && p) {
        p = p->next;
    }
    if (!p)
        return nullptr;
    auto next = p->next;
    p->next = nullptr;
    return next;
}
//合并两个有序链表的子程序即可
ListNode* merge(ListNode* l1, ListNode* l2)
{
    ListNode dummy(0);
    auto p = &dummy;
    while (l1 && l2) {
        if (l1->val < l2->val)
        {
            p->next = l1;
            p = l1;//或者写p=p->next也可以
            l1 = l1->next;
        }
        else {
            p->next = l2;
            p = l2;//或者写p=p->next也可以
            l2 = l2->next;
        }
    }
    p->next = (l1 ? l1 : l2);
    return dummy.next;
}
ListNode* sortList(ListNode* head) {
    ListNode dummy(0);
    dummy.next = head;//dummyHead
    auto p = head;
    int length = 0;
    while (p)// the length of this linkedlist
    {
        ++length;
        p=p->next;
    }

    for (int size = 1; size < length; size <<= 1)
    {
        auto cur = dummy.next;
        auto tail = &dummy;

        while (cur) {
            auto left = cur;
            auto right = cut(left, size);//left->@->@ |断开|right->@->@->@...
            cur = cut(right, size);//left->@->@|断开|right->@->@ |断开|cur->@->...
            tail->next = merge(left, right);
            while (tail->next) {
                tail = tail->next;
            }
        }
    }
    return dummy.next;
}
};

复杂度

Leetcode 152：乘积最大子序列

题目描述

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例

示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

解题思路

通过做这么多题了，看到这个题的时候，能够第一时间想到要用动态规划去完成，其思想就是遍历数组同时计算当前的最大值，然后不断更新。如果使用dp[]数组倒也能完成，但是空间复杂度太高，其实我们可以直接用一个变量直接就可以完成，这样空间复杂度将至了O(1)。

我们令imax为最大值，那么imax的递推公式可以表述如下

imax = max(imax * nums[i], nums[i]);

但是，我们的数组可能存在负值，所以会带来最大值变最小值，最小值变最大值的情况，所以我们还需要维护一个imin，其递推公式如下：

 imin = min(imin * nums[i], nums[i]);

正因为上面的原因，所以当我们当前值为负数的时候，我们需要交换一下imax和imin的值再进行计算，否则会出现混乱。

代码实现

int maxProduct(vector<int>& nums) {
    int maxvalue = INT_MIN, imax = 1, imin = 1;
    for (int i = 0; i < nums.size(); i++)
    {
        if (nums[i] < 0)
        {
            int tmp = imax;
            imax = imin;
            imin = tmp;
        }
        imax = max(imax * nums[i], nums[i]);
        imin = min(imin * nums[i], nums[i]);
        maxvalue = max(maxvalue, imax);
    }
    return maxvalue;
}

复杂度

时间复杂度为O(n)。