Leetcode 155：最小栈

题目描述

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) -- 将元素 x 推入栈中。
pop() -- 删除栈顶的元素。
top() -- 获取栈顶元素。
getMin() -- 检索栈中的最小元素。

示例

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

解题思路

看到这个题，实际上可以想到使用辅助栈来进行操作。所谓辅助栈就是用来存储每一步的最小值，数据栈自然是存储所有的数据。我们使用辅助栈和数据栈同步来做，这样的好处是思路简单，但是可能要多存一些不必要的元素。

对于push来说，这个函数操作很关键，要保证这一步辅助栈push进去的都是当前为止最小的。所以有两种情况：①辅助栈为空，自然直接push进入；②辅助栈不为空，就判断当前要push的值是否小于stack2最上面的值，如果是的话则push进去，否则不push进去。但是数据栈是直接push进去。

对于pop来说，只有数据栈和辅助栈最上面的元素一样的时候，才会pop掉辅助栈的栈顶元素。

自然，在上面的操作下，一定保证了辅助栈最上面的元素是最小的元素。所以getMin()的时候直接返回辅助栈的栈顶元素即可。

代码实现

class MinStack {
private:
    stack<int> stack1;//数据栈
    stack<int> stack2;//辅助栈
public:
    /** initialize your data structure here. */
    MinStack() {
    }
    void push(int x) {
        stack1.push(x);
        if (stack2.empty())
            stack2.push(x);
        else if (x <= stack2.top())
            stack2.push(x);
    }
    void pop() {
        if (stack1.top() == stack2.top())
            stack2.pop();
        stack1.pop();
    }
    int top() {
        return stack1.top();
    }
    int getMin() {
        return stack2.top();
    }
};

复杂度分析

时间复杂度：O(1)，“出栈”、“入栈”、“查看栈顶元素”的操作不论数据规模多大，都只是有限个步骤，因此时间复杂度是：O(1)。
空间复杂度：O(N)，这里N是读出的数据的个数。

Leetcode 160：相交链表

题目描述

编写一个程序，找到两个单链表相交的起始节点。

示例

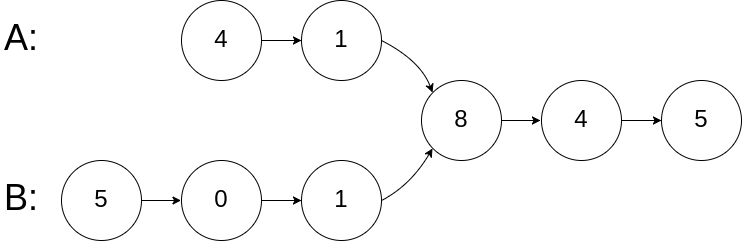
在节点8处相交。

解题思路

我这是属于一个比较傻瓜的思路。观察上图可知，我们可以考虑把两个指针放到相对于交点前移相同数目的位置作为基准进行往后移动，然后当两个指针相等的时候，就找到了它们的相交点。

那怎样实现这样呢？我们可以统计A链表的长度，假设为alen，统计B链表的长度，假设为blen，然后计算它们的差值clen。这样的话，将较长的链表的指针先往后移动clen就可以达到我们的目标了。

代码实现

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(!headA||!headB)
            return nullptr;
        ListNode *countA=headA;
        ListNode *countB=headB;
        int cA=0;
        int cB=0;
        while(countA)
        {
            ++cA;
            countA=countA->next;
        }
        while(countB)
        {
            ++cB;
            countB=countB->next;
        }
        /*将较长的链表实现最后边与较短的对齐*/
        int lLen,sLen;
        ListNode *lList;
        ListNode *sList;
        if(cA>cB)
        {
            sLen=cB;
            sList=headB;
            lLen=cA;
            lList=headA;
        }
        else
        {
            sLen=cA;
            sList=headA;
            lLen=cB;
            lList=headB;
        }
        for(int i=0;i<lLen-sLen;i++,lList=lList->next);
        
        while(lList!=nullptr&&sList!=nullptr)
        {
            if(lList==sList)
                return lList;
            lList=lList->next;
            sList=sList->next;
        }
        return nullptr;    
    }

复杂度