Leetcode 239：滑动窗口最大值

题目描述

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。

示例

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:

滑动窗口的位置 最大值
————— —–
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

解题思路

在剑指offer题目解析（2）中也曾经有这个题，我当时使用的是模拟建立一个滑动窗口，因为该方法使用了两个for循环，所以复杂度为O(n2)，这个版本在leetcode中是无法通过的。但是现在有一种新的方法可以保证算法整体时间复杂度为O(n)。

借鉴这里，实际我们并不需要每次都提取3个元素进行比较，因为实际每一次比较的3个元素，都有两个元素与前面的两个元素是重叠的（即是前一组元素减掉最前面的值），这个时候我们可以考虑采用类似于队列的方法。即需要写：

void push(int n);//在队尾插入一个元素void pop(int n);//队头元素如果是n删除它int max();//返回当前队列中的最大值

根据这个思想，写出主体框架来：

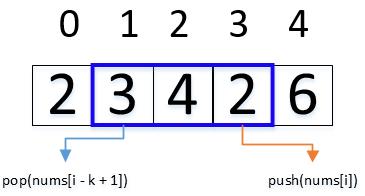
 vector<int> maxSlidingWindow(vector<int>& nums, int k) { vector<int> result; if (nums.empty()) return result; Solution win; for (int i = 0; i < nums.size(); i++) { if (i < k - 1) win.push(nums[i]);//先填满窗口前k-1个元素 else { //插入队尾元素，else后面这三句话相当于窗口滑动且找到最大值push给result win.push(nums[i]); result.push_back(win.max()); win.pop(nums[i - k + 1]); } } return result; }

接下来我们要实现各个函数的功能。

对于push来说，我们依然要在队尾添加元素，但是要把前面比新元素小的元素都删除掉。这样的话，最终单调队列中的元素就会保持一个单调递减的顺序。所以push和max都可以直接这样写：

void push(int n) { while (!data.empty() && data.back() < n) data.pop_back(); data.push_back(n); }int max() { return data.front();}

代码实现

class Solution {public: private: deque<int> deq;public: void push(int k) { while (!deq.empty() && deq.back() < k) deq.pop_back(); deq.push_back(k); } int max() { return deq.front(); } void pop(int k) { if (!deq.empty() && deq.front() == k) deq.pop_front(); } vector<int> maxSlidingWindow(vector<int>& nums, int k) { vector<int> result; if (nums.empty()) return result; Solution win; for (int i = 0; i < nums.size(); i++) { if (i < k - 1) win.push(nums[i]);//先填满窗口前k-1个元素 else { win.push(nums[i]); result.push_back(win.max()); win.pop(nums[i - k + 1]); } } return result; }};

复杂度