排序
- 外排中使用置换选择排序的目的,是为了增加初始归并段的长度。√
- 插入排序:需要有一个对比查找过程;选择排序直接插入指定位置。
- 快速排序中,第i趟排序结果至少确定i个元素的位置。
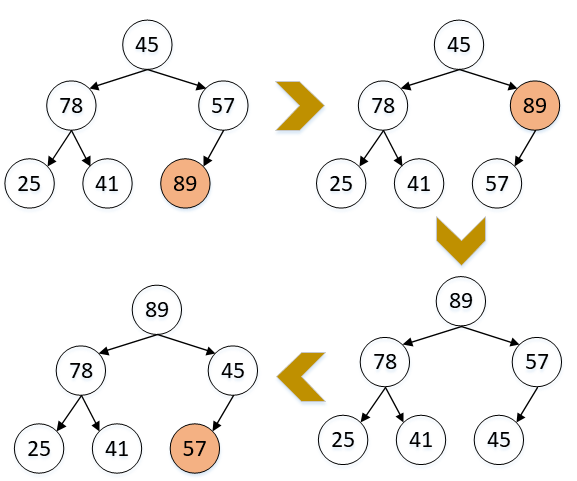
- 使用堆排序方法排序(45,78,57,25,41,89),初始堆为89,78,57,25,41,45。
- 将两个各有n个元素的有序表归并成一个有序表,最少的比较次数是n,最多是2n-1。
解析:
方法:
1. 首先将所有元素按照初始顺序填充到一个完全二叉树中
2. 从“最后一个非终端节点”开始,调用siftdown方法,调整堆的结构,直到根节点为止。
图示:
- 对于冒泡排序和插入排序来说,每一趟都能确定一个元素的最终位置。
- 设一组初始记录关键字序列为(25,50,15,35,80,85,20,40,36,70),其中含有5个长度为2的有序子表,则用归并排序的方法对该记录关键字序列进行一趟归并后的结果为( )。
解析:序列分为了5组:25,50;15,35;80,85;20,40;36,70。对前两组进行归并,得到:15,25,35,50;对第3、4组归并得到:20,40,80,85;第5组直接输出:36,70。所以最后结果是:15,25,35,50,20,40,80,85,36,70。
图
- 连通图上各边权值均不相同,则改图的最少生成树是唯一的。
- 拓扑排序反映的是一个工程能否顺利进行的问题。表示工程的有向图,顶点表示活动,弧表示活动之间的优先关系,AOV网(Activity On Vertex Network)排序算法:从AOV网中选择入度为0的顶点输出,然后删除此顶点,并删除以此顶点为尾的弧,重复直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。采用的图的数据结构:邻接表,加一个存储入度的空间。
关键路径:从源点到汇点的最长路径。 -
AOE(activity on Edge)以弧表示活动。AOV(activity on vertex network)以顶点表示活动。
- 在一个无向图中,所有顶点的度数之和等于图的边数的2倍。
- 拓扑序列和有向无环图的结构不是一一对应的。
- 设某无向图中有n个顶点e条边,则该无向图中所有顶点的度之和为2e。
- 已知无向图G有16条边,其中度为4的顶点个数为3,度为3的顶点个数为4,其他顶点的度均小于3。图G所含的顶点个数至少是11。
解析:已知图G有16条边,所以其度为32。由于计算顶点个数最少为多少,所以假设剩余的顶点度为2,这样才能保证顶点个数最少。假设度为2的顶点有x个,则可得出:4×3+3×4+x×2=32,解之得x=4。所以顶点个数为3+4+4=11个。
树
- 将森林转换为对应的二叉树,若在二叉树结点中,结点m是结点n的双亲结点的双亲结点,则在原来的森林中,m和n可能具有的关系是____。
1.父子关系
2.m的双亲结点与n的双亲结点是兄弟关系
3.兄弟关系
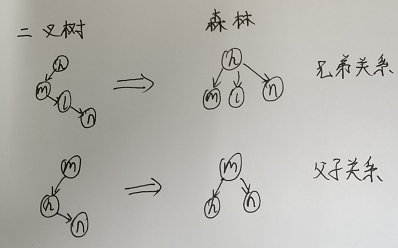
解析:若在深林中m的父结点和n的父结点是兄弟关系。那么变成二叉树后,他们形成单边右斜关系,而u和v分别在他们各自的左子树内,不可能在一条路径上,所以2是不可能的。
对于1、3来说,分别如下图:
- m阶B树的定义:

-
二叉树的线索化:对于二叉树的线索化,实质上就是遍历一次二叉树,只是在遍历的过程中,检查当前结点左,右指针域是否为空,若为空,将它们改为指向前驱结点或后继结点的线索。
前驱(pre):以中序线索二叉树的建立为例,指针pre指向中序遍历时上一个刚刚访问过的结点。 -
若度为m的哈夫曼树中,其叶结点个数为n,则非叶结点的个数为((n-1)/(m-1))
解析:哈夫曼树并不是局限于二叉树,可能也存在于多叉树。对于二叉树来说,哈夫曼树是最优二叉树(严格二叉树);对于m叉树来说,是最优m叉树(严格m叉树)。
对于度为m的哈夫曼树来说,节点的度要么为0,要么为m。设度不为零的点有a个,则总结点数为a+n。
由于除根节点外,其余每一个结点都有一个分支连向一个节点,对于度为m的每个节点都有m个分支,而度为0的节点是没有分支的,所以从分支角度来看,总的结点数是am+1。
am+1=a+n,所以a=(n-1)/(m-1)。
网络流
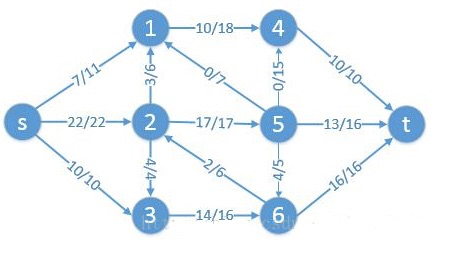
图示是一个网络流从s到t的某时刻快照。此时t处一共接收到10+13+16=39单位流量。每条横线上的数字表示当前流量和管道的容量。那么,该网络最大的流量是多少?41。
解析:
第一层为s,朝着重点最大输出为11+22+10=43。
第二层为结点1,2,3:节点一最多输出10,这是受了结点4的限制;结点2最多17,因为结点5发出最大为23;结点3最多为14,这是被结点3的入度所限制了,入度为14。所以总体是10+17+14=41。
第三层为结点4,5,6:输出为10+16+16=42。
min(43,41,42)=41。
一定要瞻前顾后(瞻前:看结点的入度是否限制;顾后:看后一结点的输出是否限制),不考虑回流。


文章评论