C++/C语言基础
- 对下列语句正确的描述是?
const int *x; //①
int * const x; //②
答案:语句②的含义是指针变量x不能更改
解析:const修饰 * 左侧的时候,表示指向的数据类型为常量;当const修饰 * 右侧的时候,表示指针本身为常量。
- 下述静态数据成员的特征中,D是错误的。
解析:
1. 静态数据成员在定义或说明时前面加关键字static。//静态变量的定义
2. 静态成员初始化与一般数据成员初始化不同。静态数据成员初始化的格式如下:
<数据类型><类名>::<静态数据成员名>=<值> //静态变量的初始化
这表明:
(1) 初始化在类体外进行,而前面不加static,(这点需要注意)以免与一般静态变量或对象相混淆。(更详细的,因为静态成员属于整个类,而不属于某个对象,如果在类内初始化,会导致每个对象都包含该静态成员,这是矛盾的。)
(2) 初始化时不加该成员的访问权限控制符private,public等。
(3) 初始化时使用作用域运算符来标明它所属类,因此,静态数据成员是类的成员,而不是对象的成员。
3.二进制数据文件流fdat读指针移到文件头的语句是:
fdat.seekg(0,ios::beg);
解析:对输入流操作:seekg和tellg;对输出流操作操作是seekp和tellp。seekg()是对输入文件定位,它有两个参数:第一个参数是偏移量,第二个参数是基地址。 对于第一个参数,可以是正负数值,正的表示向后偏移,负的表示向前偏移。而第二个参数可以是: ios::beg:表示输入流的开始位置 ios::cur:表示输入流的当前位置 ios::end:表示输入流的结束位置 tellg()函数不需要带参数,它返回当前定位指针的位置,也代表着输入流的大小。
二叉树
- n个结点的二叉链表中含有n+1(2n-(n-1)=n+1)个空指针域。利用二叉链表中的空指针域,存放指向节点在某种遍历次序下的前驱和后继结点的指针
-
若一棵完全二叉树有768 个结点,则该二叉树中叶结点的个数是384。
解析:设二叉树中度为0的节点为n0,度为1的节点为n1,度为2的节点为n2,由于n2=n0-1,所以二叉树的节点为n0+n1+n2=2n0-1+n1=768。由于n0一定为偶数个,且n1要么为0,要么为1,所以n1=1,所以n0=768/2=384。 -
设在一棵度数为3的树中,度数为3的结点数有2个,度数为2的结点数有1个,度数为1的结点数有2个,那么度数为0的结点数有(6 )个。
解析: 总结点数等于1+n1* 1+n2 * 2+n3 * 3,所以对于这个题来说,总结点数等于1+1 * 2+ 1 *2 + 3 * 2 =11,所以说,读为0的结点为11-2-1-2=6个。
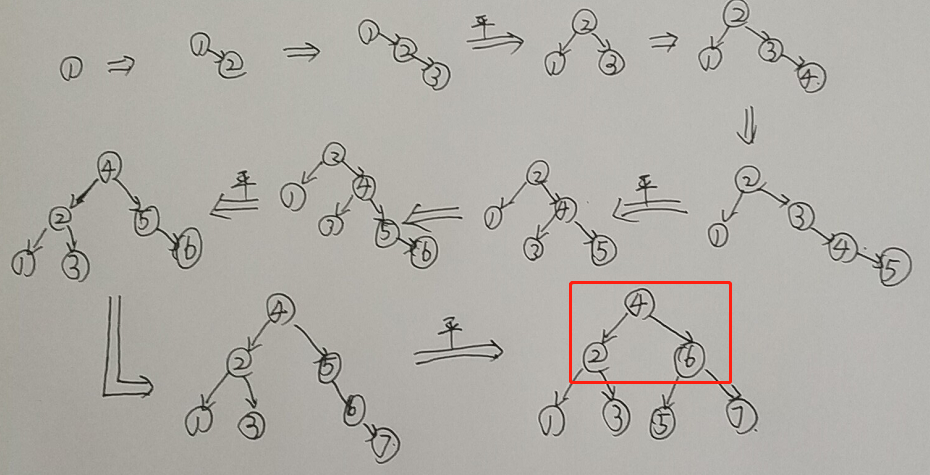
- 若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )。
解析:
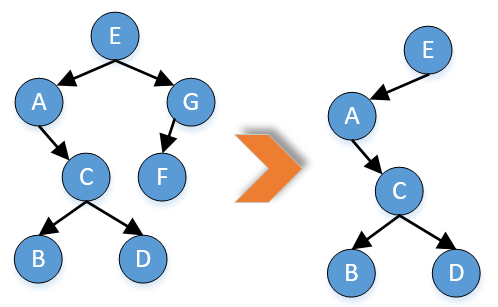
- 某二叉树结点的中序序列为A、B、C、D、E、F、G,后序序列为B、D、C、A、F、G、E。该二叉树对应的森林结点的层次序列为:E、G、A、C、D、F、B。
解析:首先是二叉树转换成森林。加入一棵二叉树的根节点有右孩子,则这颗二叉树能够转换成森林,否则将转换成一棵树。转换方法是:
(1)从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
(2)将每棵分离后的二叉树转换为树。
对于此题,结果如下:
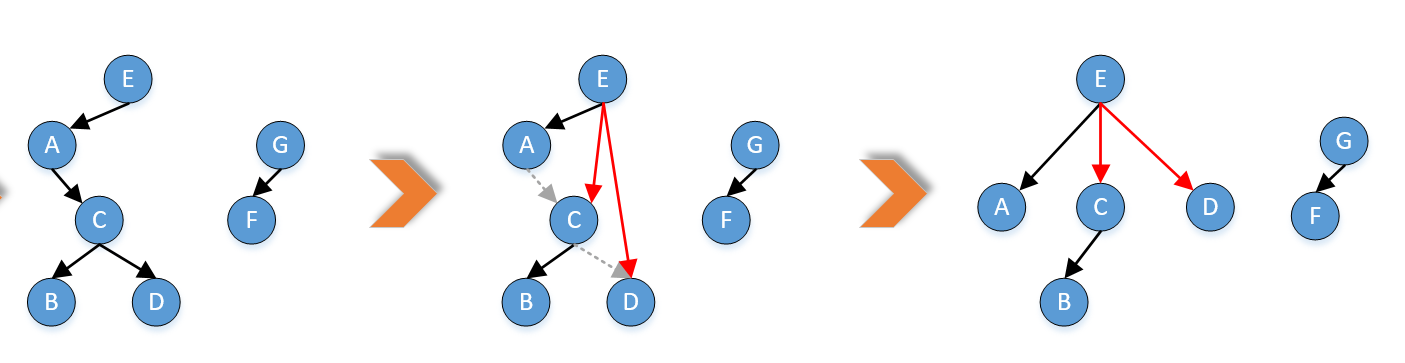
第二步是二叉树转换为树。步骤如下:
(1)加线。若某结点X的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…,都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。
(2)去线。删除原二叉树中所有结点与其右孩子结点的连线。
(3)层次调整。
对于此题,结果如下:
6. 有8个结点的无向图最多有28条边。
解析:想象邻接矩阵除去对角线一共有8 * 8-8=56个点,然后无向图,所以56/2=28。我就是忘了除以2。
- 具有n个顶点的有向图,所有顶点的出度之和为m,则所有顶点的入度之和为m。
解析:有向图的入度之和=出度之和。
8.有向图中,各列非零之和为入度,各行非零之和为出度。
- 在一个n阶B-树上,每个树根节点中所含的关键字数目最多为N-1个,最少为N/2-1(向上取整)个。
-
把一棵树转换成二叉树后,这棵二叉树的形态是唯一的。把一棵树转换成二叉树的方法如下:
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
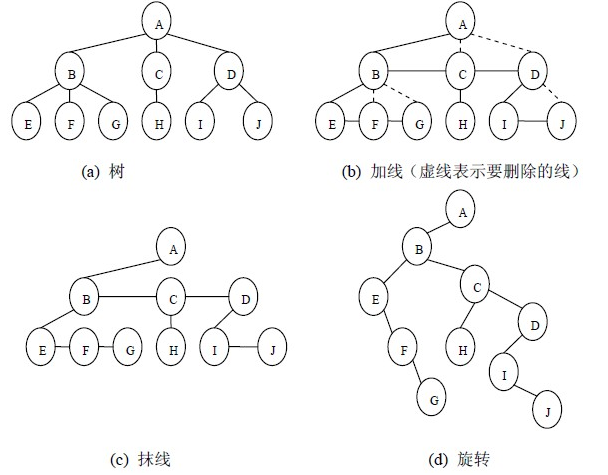
图
拓扑排序
- 已知有向图G=(V,E),其中V={ V1 , V2 , V3 , V4 , V5 , V6 , V7 },E={<V1 ,V2>, <V1 ,V3>, <V1 ,V4>, <V2 ,V5>, <V3 ,V5>, <V3 ,V6>, <V4 ,V6>, <V5 ,V7>, <V6 ,V7>}G的拓扑序列是 V1, V3, V4, V6, V2, V5, V7。
解析:
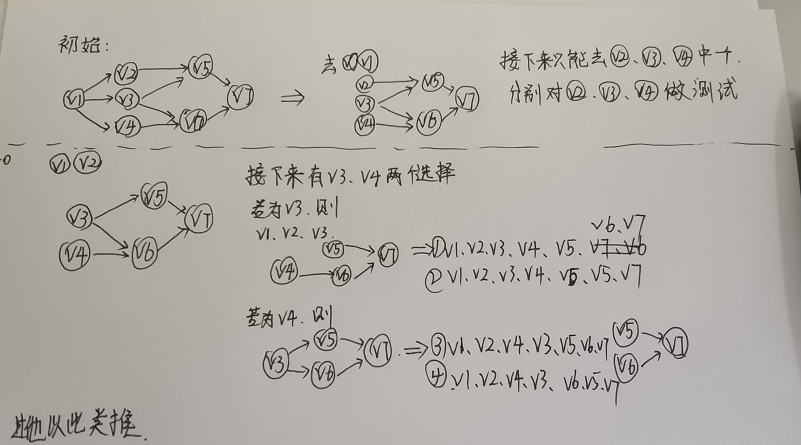
取一个结点的要求是这个结点没有任何前驱。
其它
- 用相邻矩阵A表示图,判定任意两个顶点Vi和Vj之间是否有长度为m的路径相连,则只要检查(A^m)的第i行第j列的元素是否为零即可。
解析:

机器学习
- SVM核函数主要包括:线性核函数、多项式核函数、径向基核(RBF)、傅里叶核函数、样条核、sigmoid核函数等。


文章评论