Surrounded Regions

题目描述

Given a 2D board containing'X'and'O', capture all regions surrounded by'X'.A region is captured by flipping all'O's into'X's in that surrounded region .

For example,

X X X X
X O O X
X X O X
X O X X

After running your function, the board should be:

X X X X
X X X X
X X X X
X O X X

解题思路

这道题的意思是，将边界及所有与边界相连的O予以保留，其它的O变为X。
所以我们可以采取的思路是，将边界及所有与边界相连的O先行转换成别的字母，例如S。然后遍历整个矩阵，将所有的O变为X，所有的S变为O，这样就完成了任务。

代码实现

void toS(vector<vector<char>> &board, int i, int j,int rows, int cols)
{
    if (i < 0 || j < 0 || i >= rows || j >= cols)
        return;
    if (board[i][j] == 'O')
    {
        board[i][j] = 'S';
        toS(board, i + 1, j, rows, cols);
        toS(board, i - 1, j, rows, cols);
        toS(board, i, j - 1, rows, cols);
        toS(board, i, j + 1, rows, cols);
    }

}

void solve(vector<vector<char>> &board) {
    int rows = board.size();//行数
    int cols = board[0].size();//列数
    if (rows <= 2 || cols <= 2)
        return;
    //第一行
    for (int i = 0; i < cols; i++)
    {
        if (board[0][i] == 'O')
            toS(board, 0, i,rows,cols);
    }
    //最后一行
    for (int i = 0; i < cols; i++)
    {
        if (board[rows - 1][i] == 'O')
            toS(board, rows - 1, i, rows, cols);
    }

    //第一列
    for (int i = 1; i < rows - 1; i++) {
        if (board[i][0] == 'O')
            toS(board, i, 0, rows, cols);
    }

    //最后一列
    for (int i = 1; i < rows - 1; i++)
    {
        if (board[i][cols - 1]=='O')
            toS(board, i, cols - 1, rows, cols);
    }
    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < cols; j++)
        {
            if (board[i][j] == 'O')
                board[i][j] = 'X';
            else if (board[i][j] == 'S')
                board[i][j] = 'O';
        }
    }
}

Valid-Parentheses

题目描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。
有效字符串需满足：
1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true

示例 2:

输入: "()[]{}"
输出: true

示例 3:

输入: "(]"
输出: false

示例 4:

输入: "([)]"
输出: false

示例 5:

输入: "{[]}"
输出: true

题目解析

这种匹配问题，我们有这种思想，可以用栈来解决这个问题。因为合法的匹配实际上是类似于{[()]}这样的匹配，你会发现先输入的符号相匹配的右半边是最后输入，也就是说符合栈先入后出的特性。当pop完了这个栈为空，那就说明匹配。所以我们可以设计这这样一个算法：遍历整个字符串的每一个字符，然后：
1. 如果字符是左侧符号（如{``(``[）那么我们就向堆栈里面push进去；
2. 当字符不是左侧符号的时候，首先要判断堆栈此时是否为空，若为空返回false，因为左侧符号还未匹配完；如果栈不为空，判断此时栈顶元素是否与当前元素相等，若不相等，也返回flase；若相等，pop出来，继续走下去。
3.当所有字符遍历完，这个时候判断栈是否为空，若为空说明都匹配，返回true，否则返回false。

代码实现

bool isValid(string s) {
    int slen = s.size();
    if (slen == 0)
        return true;
    if (slen < 2)
        return false;
    stack<char>cstack;
    for (int i = 0; i < slen; i++)
    {
        if (s[i] == '(')
            cstack.push(')');
        else if (s[i] == '[')
            cstack.push(']');
        else if (s[i] == '{')
            cstack.push('}');
        else if (cstack.empty() || cstack.top() != s[i])
            return false;
        else
            cstack.pop();
    }
    return cstack.empty();

}

remove-nth-node-from-end-of-list

题目描述

Given a linked list, remove the n th node from the end of list and return its head.

Given linked list: 1->2->3->4->5, and n = 2.

After removing the second node from the end, the linked list becomes 1->2->3->5.

Note: Given n will always be valid.Try to do this in one pass.

解题思路

要求只能走一次路径，所以启发我们使用快慢指针。由于给予n总是合法的，所以我们不需要判断n是否超过链表长度（如果需要判断的话，必然不可能只走一趟）。

假设我们的链表是1->2->3->4->5，且n=2。那么我们初始状态下，链表如下：

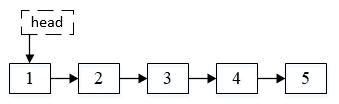
第一步，首先建立一个头指针，命名为dummy，算是一个pivot，然后令head也指向这个dummy。
第二步，新建快指针pfast、慢指针pslow，然后分别指向dummy。
到目前为止，链表关系如下图所示：

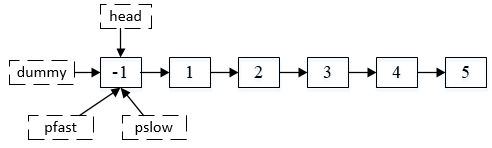
第三步，这一步很关键。就是后移pfast指针n个位置，在这里就是2个位置。结果如下：

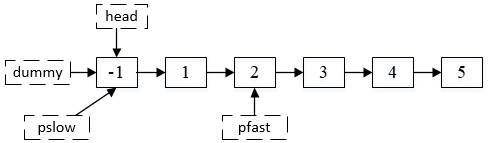
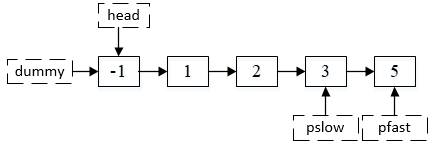
第四步，在完成上述操作之后，开始同时移动pfast和pslow，直到pfast的next指针为空的时候停止移动。这个时候的结果如下：

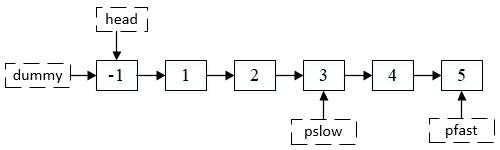
第五步，我们新建一个链表指针指向pslow的next，命名为delp节点，这就是我们待删除的位置。然后令pslow的next指向5的地址（pslow->next=pslow->next->next）。
第六步，删除delp节点，也就是执行delete(delp)命令。
最后，返回dummy->next即可。结果如下：

代码实现

ListNode *removeNthFromEnd(ListNode *head, int n) {
    if (head == NULL)
        return head;
    ListNode *dummy = new ListNode(-1);
    dummy->next = head;
    head = dummy;
    ListNode *pslow = head;
    ListNode *pfast = head;
    while (n--)
    {
        pfast = pfast->next;
    }
    while (pfast->next != NULL)
    {
        pslow = pslow->next;
        pfast = pfast->next;
    }
    ListNode *delp = pslow->next;
    pslow->next = pslow->next->next;
    delete delp;
    return dummy->next;

}