Leetcode 39:组合总和
题目描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
示例
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
题目解析
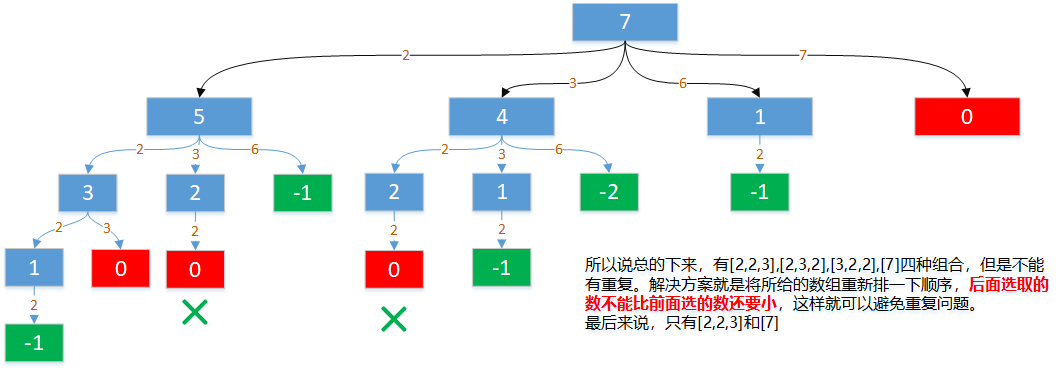
代码实现
class Solution {
public:
private:
vector<int> candidates;
vector<int> path;
vector<vector<int>> res;
public:
void DFS(int start, int target)
{
if(target==0)
{
res.push_back(path);
return ;
}
for(int i=start;i<candidates.size()&&target-candidates[i]>=0;i++)
{
path.push_back(candidates[i]);
DFS(i,target-candidates[i]);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
this->candidates=candidates;
DFS(0,target);
return res;
}
};
复杂度
Leetcode 42:接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解题思路
这个题目的想法,最容易想到的就是将它以最高的地方为基准分为左右两列进行相加计算,因为相加不可能跨过最高的那个地方。
对于左侧,我们从0向最高值靠拢,首先判断当前位置的值是否小于left(left刚开始是第0个,判断从第0个开始判断没问题),如果小于,那么就将suml累加上left-A[i]即可,如果不是小于,那么代表着从这一点开始,又要重新计算一个容量,所以令left=A[i]。如下所示:
if (A[i] < left)
suml += left - A[i];
else
left = A[i];
对于右侧同理,从最右侧n-1开始往左判断,过程与上面相同,不再重复。代码如下:
if (A[i] < right)
sumr += right - A[i];
else
right = A[i];
代码实现
int trap(vector<int>& height) {
int n = height.size();
int maxHeight = 0;
int left = 0;//由左往最大值计算
int right = 0;//反向
int suml = 0, sumr = 0;
//寻找最大高度
for (int i = 0; i < n; i++)
if (height[i] > height[maxHeight])
maxHeight = i;
//寻找到最大高度了。先计算最侧的最大容量
for (int i = 0; i < maxHeight; i++)
{
if (height[i] < left)
suml += left - height[i];
else
left = height[i];
}
//再计算右侧
for (int i = n - 1; i > maxHeight; i--)
{
if (height[i] < right)
sumr += right - height[i];
else
right = height[i];
}
return suml + sumr;
}
复杂度
时间复杂度:O(n)
空间复杂度:O(1)
Leetcode 33:搜索旋转排序数组
题目描述
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
解题思路
可以想到利用二分法去做,但是我做的用时还是太高。这里展示一个leetcode的一个4ms执行用时的代码,把条件用了异或符号来表示,这种表示方法还是很不错的。
代码实现
int search(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size() - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (nums[mid] == target)
{
return mid;
}
else if ((nums[0] > target) ^ (nums[0] > nums[mid]) ^ (target > nums[mid]))
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return -1;
}
复杂度
时间复杂度:O(logn)
空间复杂度:O(1)
Leetcode 34:在排序数组中查找元素的第一个和最后一个位置
题目描述
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
解题思路
很明显,使用二分法,具体细节见代码即可。
代码实现
vector<int> searchRange(vector<int>& nums, int target) {
vector<int>result(2, -1);
if (nums.empty())
return result;
int l = 0, r = nums.size() - 1;
if (nums[l] > target || nums[r] < target)
return result;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target)
r = mid;
else
l = mid + 1;
}
if (nums[l] == target)
result[0] = l;
r = nums.size();
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] > target)
r = mid;
else
l = mid + 1;
}
if (nums[l - 1] == target)
result[1] = l - 1;
return result;
}
复杂度
时间复杂度:O(nlogn),空间复杂度:O(1)



文章评论