valid sudoku

题目描述

Determine if a Sudoku is valid, according to: Sudoku Puzzles - The Rules.The Sudoku board could be partially filled, where empty cells are filled with the character'.'.

题目解析

数独具有以下规则：

• 每一行所有元素不能重复（1~9）；
• 每一列所有元素不能重复（1~9）；
• 由第3i~3(i)+2行和第3i~3(i)+2列组成的九宫格内元素不能重复（其中0<=i<n/3-1，元素仍为1~9）。

想到重复问题，自然而然我们想到了设置Flag的方法，由此我们可以设置3个n×n大小的矩阵来作为标志位：

• 第一个矩阵命名为fRow，作为判断每一行的数字是否重复的矩阵，因为元素只能为1~9，所以正好每行9个格子合适。
• 第二个矩阵命名为fCol，作为判断每一行列的数字是否重复的矩阵，因为元素只能为1~9，所以正好每行9个格子合适。
• 第三个矩阵命名为fMat，作为判断每个九宫格的数字是否重复的矩阵。

本题的特殊之处在于允许有空格的格子，且空格的地方以字符.表示，且所存储的数字都是char类型，因此首先要进行一个类型转换才能判断：

if(board[i][j] >= '1' && board[i][j]<='9')
    int temp = board[i][j]-'1';

若检测到该行出现这个数字，则设置该行这个位置为true，当又遍历到这个数字的时候，若检查发现这个位置已经设置为true了，则返回false。当然在实现代码的时候，要把判断放在前面，把设置标志位放在后面。

该方法的时间复杂度为O(n2)，空间复杂度为O(n2)。

代码实现

bool isValidSudoku(vector<vector<char> > &board) {
        int totalRows = board.size();
        int totalCols = board[0].size();
        if(totalRows == 0 || totalCols == 0)
            return false;
        vector<vector<bool> > fRow(totalRows,vector<bool>(totalCols,false));//行标志矩阵
        vector<vector<bool> > fCol(totalRows,vector<bool>(totalCols,false));//列标志矩阵
        vector<vector<bool> > fMat(totalRows, vector<bool>(totalCols,false));//9宫格标志矩阵
        for(int i = 0;i < totalRows; i++)
        {
            for(int j = 0; j < totalCols; j++)
            {
                if(board[i][j] >= '1' && board[i][j]<='9')
                {
                    int temp = board[i][j]-'1';
                    if(fRow[i][temp] || fCol[temp][j] || fMat[3*(i/3)+j/3][temp])
                        return false;
                    fRow[i][temp] = true;
                    fCol[temp][j] = true;
                    fMat[3*(i/3)+j/3][temp] = true;
                }
            }
        }
        return true;
    }

largest rectangle in histogram

题目描述

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

For example,Given height =[2,1,5,6,2,3],return10.

题目解析

我们以[2,1,5,6,2,3]为例来思考这个题目的思想。观察如图所示。

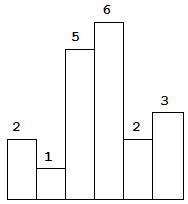
代码实现

int largestRectangleArea(vector<int> &height) {
    int maxarea = 0;
    stack<int>stk;
    for (int i = 0; i < height.size(); i++)
    {
        //如果堆栈是空的或者堆栈里面的最大数小于当前数组的元素，则当前数组元素入栈
        if (stk.empty() || stk.top() <= height[i])
            stk.push(height[i]);
        else {
            //如果堆栈非空且栈顶元素大于当前元素的话
            int count = 0;
            while (!stk.empty() && stk.top() > height[i])
            {
                count++;
                maxarea = max(maxarea, stk.top()*count);
                stk.pop();
            }
            while (count--)
                stk.push(height[i]);
            stk.push(height[i]);
        }

    }
    int count = 1;
    while (!stk.empty())
    {
        maxarea = max(maxarea, stk.top()*count);
        stk.pop();
        count++;
    }
    return maxarea;

}

pascals-triangle-ii

题目描述

Given an index k, return the k th row of the Pascal's triangle.For example, given k = 3,
Return[1,3,3,1].

题目解析

代码实现

vector<int> getRow(int rowIndex) {
    vector<vector<int> > tempresult(rowIndex+1);//传回的二维数组
    vector<int> result;
    for (int i = 0; i <= rowIndex; ++i)
    {
        tempresult[i].push_back(1);
        for (int j = 1; j < i; j++)
            tempresult[i].push_back(tempresult[i - 1][j - 1] + tempresult[i - 1][j]);
        if (i > 0)
            tempresult[i].push_back(1);
    }
    return tempresult[rowIndex];
}

Construct binary tree from preorder and inorder traversal

题目描述

Given preorder and inorder traversal of a tree, construct the binary tree.
Note: 
You may assume that duplicates do not exist in the tree.

思路

关于根据前序和中序如何得到二叉树的结构的计算方式，我就不重复了，之前的程序里面也有，这里就只说说代码里几个参数的思路。
**一定要做边界条件的判断！***

    root->left = build(preorder, pstart + 1, pstart + i - istart, inorder, istart, i - 1);
    root->right = build(preorder, pstart + i - istart + 1, pend, inorder, i + 1, iend);

对于左子树处理来说，中序遍历所要处理的位置就是根节点左侧的所有数字，所以自然起始位置就是istart，结束位置就是i-1；对于前序遍历来说表示就麻烦一些，起始位置还好，是pstart+1,结束位置是pstart+(i-istart)，其中i-istart是左子树的元素数。
对于右子树处理来说，中序遍历所要处理的位置就是根节点右侧的所有数字，所以自然起始位置就是i+1，结束位置就是iend；对于前序遍历来说，就是从左侧子树最后一个元素后面那个数字到最后一个，所以起始位置是pstart + i - istart + 1，结束位置是pend。

代码实现

TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
    int presize = preorder.size();
    int insize = inorder.size();
    if (presize == 0 || insize == 0)
    {
        return NULL;
    }
    else if (presize != insize)
        return NULL;
    return build(preorder, 0, presize - 1, inorder, 0, insize - 1);
}

TreeNode* build(vector<int>&preorder, int pstart, int pend, vector<int>&inorder, int istart, int iend)
{
    if (pstart > pend || istart > iend)
        return NULL;
    int mid = preorder[pstart];
    TreeNode* root = new TreeNode(mid);
    int i = istart;
    for (; i <= iend; ++i)
    {
        if (inorder[i] == mid)
            break;
    }

    root->left = build(preorder, pstart + 1, pstart + i - istart, inorder, istart, i - 1);
    root->right = build(preorder, pstart + i - istart + 1, pend, inorder, i + 1, iend);
    return root;
}