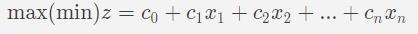线性规划问题 遇到一个线性规划问题，该如何解决呢？ 1. 确定决策变量。 2. 确定目标函数。 3. 找出约束条件。 4. 求最优解。 一般线性规划问题可以表示为如下形式。 约束条件为： 变量满足约束条件的一组值成为线性规划问题的一个可行解。 所有可行解构成的集合成为线性规划的可行区域。 使目标函数取得极值的可行解称为最优解。 在最优解处目标函数的值成最优值。 线性规划解的情况： - 有唯一最优解。 - 有无数多个最优解。 - 没有最优解。 线性规划的标准型 标准型如下： 四个要求： 目标函数为最大值（即为max）…
按照环境保护部《建设项目环境影响评价政府信息公开指南（试行）》的要求，我厅将2018年11月12日环境影响评价文件受理情况进行公开，并征求公众意见。 一、征求意见日期：2018年11月12日－2018年11月26日（10个工作日） 二、征求意见期间，省生态环境厅接受反映2018年11月12日受理的建设项目环境影响评价文件情况和问题的来信、来访和来电。 三、联系方式： 电话：0531－82083172 电子信箱：sdhbhpc@shandong.cn 通讯地址：济南市市中区站前路9号1号楼4层山东省政务服务中心建设投…
由于今天只是初步安装，没有牵扯到主题和插件等其他方面的问题，因此现在问题就很基础。寒假会不断更新的。 1.如果想在Git Page中加入我自己做的静态页面该怎么呢？ 需要将该网页放入source目录之中。但是仅仅这一步是不够的，因为如果仅仅这样，发布以后会发现，这个网页的代码被修改了，外层嵌套上了Hexo主题页面的代码。这个怎么办呢？ 这就需要修改_config.yml中的skip_render。修改格式如下（目录是相对于source来说）： skip_render: - test/** 这个代表的意思是不渲染t…
张玉帅2018年9月—2019年1月总体规划 （2018年9月9日制定第1版） 一、本学期总体计划安排 1.高水平、高质量完成老师交代各项任务和工作； 2.高水平、高质量、高要求完成毕业设计开题相关任务； 3.完成C++语言基本语法学习； 4.完成计算机组成原理学习； 5.复习操作系统原理基本知识； 6.开始系统学习算法知识（从明年1月份开始，暂定以《趣学算法》为书籍）。 二、任务分解 （一）9月份任务分解 1.完成C++语言基本语法学习。具体时间安排如下： 课程内容 第1-3周课程 第4-6周课程 第7-9周课程…
其实我的博客从上一次发文章介绍更新之后也更新过好多次了，但是大部分情况下都是只换一个好看的模板而已，这也是由于上大学之后忙于学习所以很少打理博客的原因。所以博客的访问量也急剧下降了。 最近一段时间一直在思考自己研究生的生活应该怎样度过，思考来思考去，最后还是决定踏踏实实做科研，努力把自己转型到偏向于Deep Learning方向的算法工程师，所以这需要长时间的学习和总结。为此，我制定了结合博客和个人公众号来督促自己发布学习总结和知识总结的任务。为了配合这个任务，我对博客进行了大规模彻底的改版。改版的地方主要有以下几…
时间：2018年8月1日 18:00 地点：山东·济南·鲁能大球场 观众人数：25147人 结果：山东鲁能泰山3:1上海绿地申花
第二周：网络爬虫之提取 2.1BeautifulSoup库入门 1.使用BeautifulSoup的方式 from bs4 import BeautifulSoup soup = BeautifulSoup(‘<p>data</p>’, ‘html.parser’) 第一个参数是一个html格式的信息。 2. BeautifulSoup的基本元素 BS库是解析、遍历、维护“标签树”的功能库。例如： soup = …
最近评论
davidcheung 发布于 6 个月前（02月09日）
tk88 发布于 6 个月前（02月07日）
cuicui 发布于 9 个月前（10月20日）
niming 发布于 10 个月前（09月19日）
davidcheung 发布于 2 年前（08月16日）
Nolan 发布于 2 年前（07月25日）
davidcheung 发布于 3 年前（06月19日）
aobai 发布于 3 年前（03月13日）
匿名 发布于 5 年前（12月30日）
小奥 发布于 5 年前（12月12日）