Leetcode 96：不同的二叉搜索树

题目描述

给定一个整数n，求以1…n为节点的二叉搜索树有多少种？

示例

解题思路

可以使用动态规划解，但是这个题同样也是一个卡塔兰数问题。卡塔兰数的应用主要有：找零钱问题、三角网格问题、括号排列问题、球盒问题等。卡塔兰数的数学表达式为

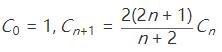
所以代码只需要实现这个式子即可，时间复杂度为O(n)，空间复杂度为O(1)。

代码实现

int numTrees(int n) {    long long C = 1;    for (int i = 0; i < n; ++i)    {        C = C * 2 * (2 * i + 1) / (i + 2);    }    return (int)C;}

复杂度分析

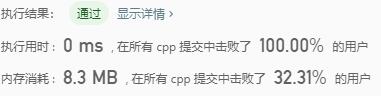
时间复杂度为O(n)，空间复杂度为O(1)。

Leetcode 98：验证二叉搜索树

题目描述

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

题目解析

二叉树的题一般比较容易想到的就是用递归去做，在这里我们用一个名为vBST的子函数去做，由于是二叉搜索树，它的特征就是：

• 节点的左子树只包含小于当前节点的数；
• 节点的右子树只包含大于当前节点的数。

所以在这个子函数里面我们要传三个参数：当前结点、如果是二叉搜索树时的最小值和最大值。那么对于这三个值，我们分别假设为value、lower和upper。这样就存在三种情况：当前结点为空，那么自然返回true；若lower值存在（若是判断根节点等情况下，lower值可能不存在，所以传递的时候要传递一个可取值的最小值，由于示例中给出了超过int类型的数值，所以这里我们使用了long long类型），那么value小于lower的话，说明当前结点小于其根结点的值，自然不是二叉搜索树，返回false；同理对upper也是如此。如果当前值符合要求，则一层一层递归下去即可。

代码实现

bool vBST(TreeNode* root, long long lower, long long upper){    if (root == nullptr)        return true;    int value = root->val;    if (lower != LLONG_MIN && value <= lower)        return false;    if (upper !=LLONG_MAX && value >= upper)        return false;    return (vBST(root->left, lower, value) && vBST(root->right, value, upper));}bool isValidBST(TreeNode* root) {    if (root == nullptr)        return true;    return vBST(root, LLONG_MIN, LLONG_MAX);}

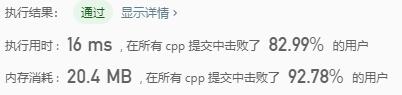
执行用时&内存消耗