Leetcode 105：重建二叉树

题目描述

根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。

示例

给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

3

/ \
9 20
/ \
15 7

题目解析

我们根据前序遍历的特点可以发现，前序遍历的第一个数字一定是这个二叉树的根节点；然后根据中序遍历的特点可发现，根节点左侧的数字一定是左子树，右侧一定是右子树。然后将中序遍历以根节点为中心划分成两个部分，这又是两个子树，然后这个子树又可以根据前序遍历找到各个子树的根节点……以此类推，这非常适合有递推来实现。

就拿这个例子来说。

前序遍历：

序号	0	1	2	3	4	5	6	7
内容	1	2	4	7	3	5	6	8

中序遍历：

序号	0	1	2	3	4	5	6	7
内容	4	7	2	1	5	3	8	6

这又就把中序遍历分为了4/7/2和5/3/8/6两个部分。然后考虑4/7/2这个部分，前序遍历的第2个数字是划分4/7/2的数字，这样，2是这个子树的根节点，4/7都位于左子树。

然后再看右子树，也就是3/5/6/8这四个数字。同理可以得出，3是右子树的根节点，然后5在左子树，8/6在右子树。再去8/6这个子树看，根据前序遍历可以看到6为子树的根节点，根据中序遍历可以看到，8为子树的左结点。

接下来考虑代码实现问题。首先肯定要判断所给的两个数组是不是空，若是空肯定是个空树，否则继续进行。我们可以使用类里面的一个私有函数来进行具体的重建功能，而这个函数的参数自然是前序遍历结果、起始位置、结束位置、中序遍历结果、起始位置、结束位置。

当然作为刚开始的时候，起始位置肯定是0，结束位置肯定是length-1。

使用这个私有函数进行递归，肯定有停止递归的条件，那就是开始位置大于结束位置的时候，自然就代表迭代结束了。

然后新建一个TreeNode，第一个节点自然是前序遍历的第一个节点，所以可以：

TreeNode root=new TreeNode(pre[startPre]);

接下来自然要开始进行判断，寻找前序遍历和中序遍历相等值的位置，由于前序遍历里面的点都可以作为中序遍历里面的根节点，所以我们只需要在中序遍历里面找到与前序遍历中值相等的位置，就是该子树的根节点的位置，就可以根据这个点划分左子树和右子树了。而中序遍历中到的根节点的位置i左侧有几个数字就是左子树有几个元素，右边有几个数字就是右子树有几个元素

对于左子树来说，左子树的起始位置自然是startPre的下一个位置，而结束是startPre+i-startIn（startPre是位置，i-startIn是从中序遍历中看左子树有几个元素），而中序遍历的开始位置自然是startIn，结束位置是i-1。

对于右子树来说，中序遍历的起始位置自然是i+1，结束位置是endIn；而对于前序遍历来说，自然是startPre+左子树的元素数+1，而左子树我们知道是i-startIn了，所以起始位置是startPre+i-startIn+1，结束位置自然是endPre。

于是，完成了这个程序的编写。

代码实现

TreeNode* build(vector<int>& pre, int ps, int pe, vector<int>& in, int is, int ie)
{
    if (ps > pe || is > ie)
        return nullptr;
    int mid = pre[ps];//找到中序遍历的中间结点
    TreeNode* root = new TreeNode(mid);
    int i = is;
    for (; i <= ie; ++i)
    {
        if (in[i] == mid)
            break;
    }
    root->left = build(pre, ps + 1, ps + i - is, in, is, i - 1);//对左子树下手
    root->right = build(pre, ps + i - is + 1, pe, in, i + 1, ie);//对右子树下手
    return root;
}


TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    int presize = preorder.size();
    int insize = inorder.size();
    if (presize == 0 || insize == 0)
        return nullptr;
    else if (presize != insize)
        return nullptr;
    return build(preorder, 0, presize - 1, inorder, 0, insize - 1);
}

复杂度

Leetcode 114：二叉树展开为链表

题目描述

给定一个二叉树，原地将它展开为链表。

题目解析

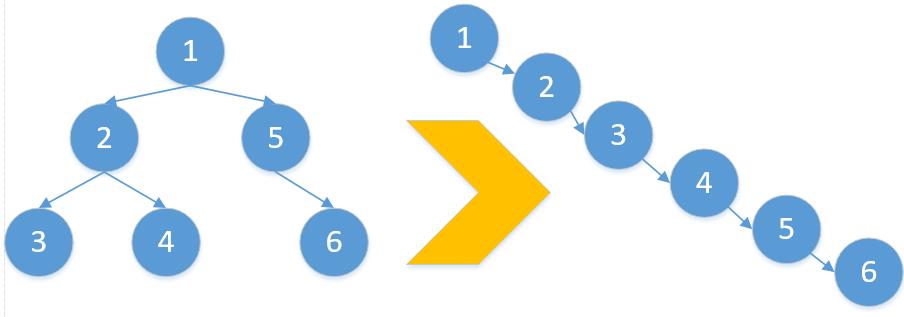
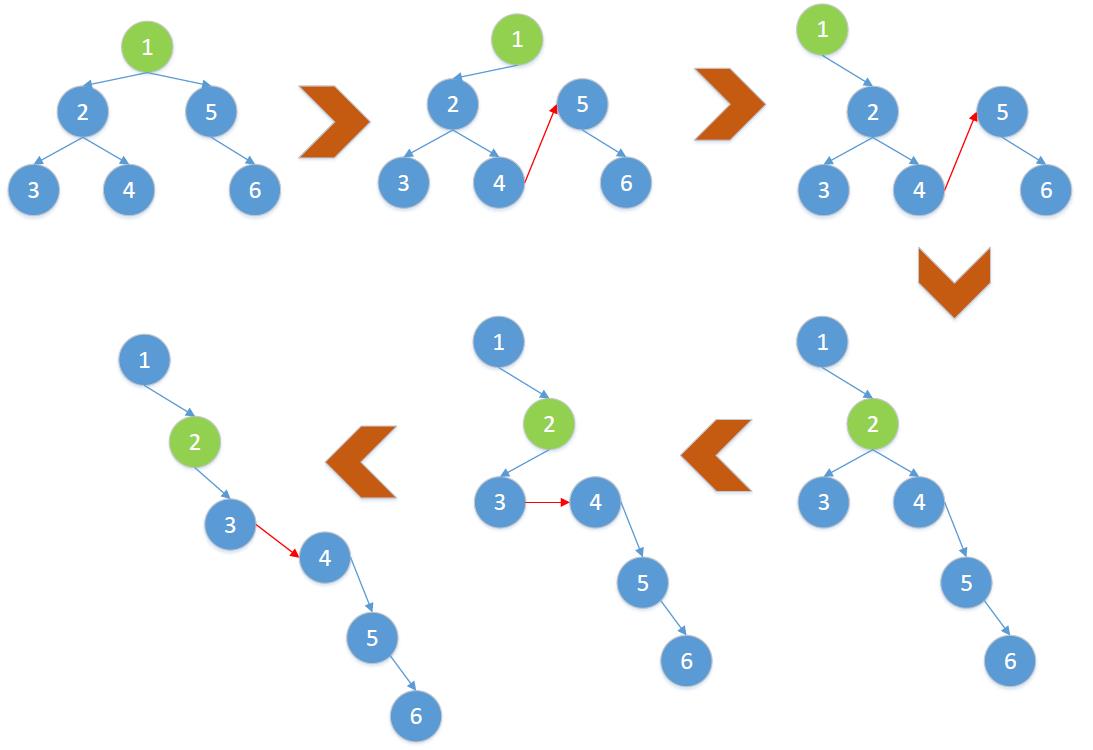
我们以上图来考虑该如何去做。其整个过程如下图所示。首先确定根节点，然后寻找左子树的最右节点，将右子树挂在这个最右节点上，然后把左子树挂在右子树的位置上，最后将左子树置为空。这样便完成了一个循环。

然后将根结点指针往后移一个节点，继续下一个过程。如果该结点的左子树是空，那么就直接进入下一个过程。如果这个时候当前节点已经是空了，那么代表整个任务已经完成了。

代码实现

void flatten(TreeNode* root) {
    while (root != nullptr) {
        if (root->left != nullptr) {
            auto mright = root->left;//如果左子树非空，找左子树的最右节点
            while (mright->right != nullptr)
                mright = mright->right;
            //找完
            mright->right = root->right;//把根的右孩子挂载左子树最右节点的右子树上
            root->right = root->left;//这个时候根的右孩子可以无视了，把左孩子放到右孩子上
            root->left = nullptr;//左子树置空即可
        }
        root = root->right;//下一步继续进行
    }
}

复杂度