Leetcode 207:课程表
题目描述
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
解题思路
这个题目是一个图的问题,所给的示例是用边缘列表来表示的图。也即假如边缘列表表示如下
| 序号 | 节点1 | 节点2 |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 0 |
所表示的图为
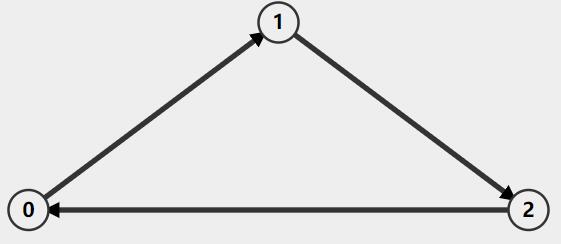
可以发现上图就是一个无法实现课程的图,这类的特点是它是一个有向有环图。
所以这个问题可以转换为另一个问题:如何判断一个图是有向无环图?
使用拓扑排序如下:
- 首先新建一个入度表
indegrees,用于记录每个节点的入度。 - 新建一个队列
que,用于存储入度为0的节点。 - 当queue非空,一次将首节点出队,在图中删除此节点pre,并将
--numCourses。当然,我们不是真正从邻接表中删除pre,而是将indegrees[cur]-=1;当入度-1邻接节点cur的入度为0的时候,说明cur所有前驱结点已经删除,可以入队。 - 若是有向无环图,则所有节点一定入队并且出队过,即若存在环的话,一定有节点入度始终不为0,即numCourses大于0。所以判断
numCourses==0即可判断出是否是有向无环图。
代码实现
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) { if(prerequisites.empty()) return true; vector<int> indegrees(numCourses, 0);//新建入度表 for (int i = 0; i < prerequisites.size();i++) { ++indegrees[prerequisites[i][0]]; }//统计每一个节点入度 queue<int> que;//新建一个队列,用于存储入度为0的节点 for (int i = 0; i < numCourses; i++) { if (indegrees[i] == 0) que.push(i); }//借助一个队列,将入度为0的节点入队 while (!que.empty()) { int pre = que.front(); que.pop(); --numCourses;//在每次pre出队的时候,执行--numCourses //当queue非空,一次将首节点出队,在图中删除此节点pre for (auto req : prerequisites) { if (req[1] != pre) continue; if (--indegrees[req[0]] == 0) que.push(req[0]); } //并不是真正从邻接表中删除pre,而是将indegrees[cur]-=1 //当入度-1邻接节点cur的入度为0的时候,说明cur所有前驱结点已经删除,可以入队。 } //若是有向无环图,则所有节点一定入队并且出队过,即若存在环的话,一定有节点入度始终不为0,即numCourses大于0 //所以判断numCourses==0即可 return numCourses == 0;}复杂度

复杂度挺高的
Leetcode 208:实现Trie(前缀树)
题目描述
实现一个 Trie (前缀树),包含insert, search, 和 startsWith 这三个操作。
示例
Trie trie = new Trie();trie.insert("apple");trie.search("apple"); // 返回 truetrie.search("app"); // 返回 falsetrie.startsWith("app"); // 返回 truetrie.insert("app"); trie.search("app"); // 返回 true解题思路
Trie树的结点结构
Trie树是一个有根的树,其结点具有以下字段:。
最多 R个指向子结点的链接,其中每个链接对应字母表数据集中的一个字母。
本文中假定 R为26,小写拉丁字母的数量。布尔字段,以指定节点是对应键的结尾还是只是键前缀。
向Trial插入字符串
我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况:
- 如果链接已经存在。那么沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
- 如果链接不存在。创建一个新的节点,并将它与父节点的链接相连,该链接与当前的键字符相匹配。
重复以上步骤,直到到达键的最后一个字符,然后将当前节点标记为结束节点,算法完成。
时间复杂度:O(m),其中m为键长。在算法的每次迭代中,我们要么检查要么创建一个节点,直到到达键尾。只需要 m次操作。
空间复杂度:O(m)。最坏的情况下,新插入的键和 Trie 树中已有的键没有公共前缀。此时需要添加 m 个结点,使用 O(m)空间。
查找Trial中的字符串
这个思路很简单。每个键在Trie树种都表示从根到内部结点或者叶的路径。我们用第一个键字符开始,检查当前结点与建字符对应的链接,其有两种情况:
- 存在链接。继续往下一个结点走,如此循环。
- 没有链接。再看isStr是否是True,是则返回true,否则就返回false。
时间复杂度:O(m),空间复杂度O(1)。
查找Trie中的键前缀
类似于前面的方法,但是到达键前缀的末尾时,总是返回true。理由也很简单,我们只是为了寻找与键前缀相匹配的字符串而已,并不是完全相等的字符串。
时间复杂度:O(m),空间复杂度O(1)。
参考:https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/
代码实现
const int MAXN = 26;class Trie {public: bool isStr;//当前结点是否为一个完整的字符串 Trie* next[MAXN]; /** Initialize your data structure here. */ Trie() { isStr = NULL; memset(next, 0, sizeof(next)); } /** Inserts a word into the trie. */ void insert(string word) { Trie* cur = this;//cur初始化为根节点指针 for (char w : word) {//遍历word中每一个字符 if (cur->next[w - 'a'] == NULL)//下一个结点不存在,新增一个结点 { Trie* nnode = new Trie(); cur->next[w - 'a'] = nnode; } cur = cur->next[w - 'a']; } cur->isStr = true;//当前结点已经是一个完整的字符串 } /** Returns if the word is in the trie. */ bool search(string word) { Trie* cur = this; for (char w : word) { if (cur != NULL) cur = cur->next[w - 'a'];//更新cr指针的指向,指向下一个结点 } return (cur != NULL && cur->isStr); } /** Returns if there is any word in the trie that starts with the given prefix. */ bool startsWith(string prefix) { Trie* cur = this; for (char w : prefix) { if (cur != NULL) cur = cur->next[w - 'a'];//同上 } return (cur != NULL); }};复杂度分析

