Leetcode 215:数组中的第K个最大元素
题目描述
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
解题思路
偷了个懒,就是利用求第k个小的数字改的。因为求第k个大的数字和求第m个小的数字有以下关系(假设数组长度为len):m=len-k+1,所以直接进行转换即可。
代码实现
int partition(vector<int>& nums, int left, int right)
{
int start = left;
int end = right;
int poivt = nums[start];
while (start < end)
{
while (start < end && nums[end] >= poivt)
--end;
nums[start] = nums[end];
while (start < end && nums[start] < poivt)
++start;
nums[end] = nums[start];
nums[start] = poivt;
}
return start;
}
int findKthLargest(vector<int>& nums, int k) {
int nlen = nums.size();
int m = nlen-k+1;
if (nlen < 1 || nlen < m)
{
return -1;
}
int start = 0;
int end = nlen - 1;
int target = 0;
while (start <= end)
{
int mid = partition(nums, start, end);
if (mid == m - 1)
{
target = nums[mid];
break;
}
else if (mid > m - 1)
end = mid;
else
start = mid + 1;
}
return target;
}
复杂度分析
时间复杂度:O(nlogn)
Leetcode 221:最大正方形
题目描述
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例
输入:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
输出: 4
解题思路
参考官方题解,步骤如下:
- 我们用 0 初始化另一个矩阵 dp,维数和原始矩阵维数相同;dp(i,j) 表示的是由 1 组成的最大正方形的边长。
- 从 (0,0)(0,0) 开始,对原始矩阵中的每一个 1,我们将当前元素的值更新为
dp(i, j)=min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1
- 我们用一个变量记录当前出现的最大边长,这样遍历一次就可以找到正方形的最大边长maxr,返回的结果就是
maxr*maxr。
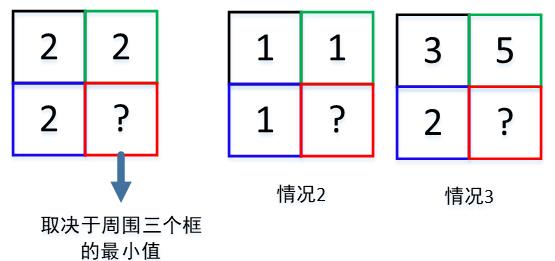
由于动态规划可以分解为若干个独立的子问题,由于一个格子的值受其左侧、左上角和上侧三个点来决定,所以我们以四个格子举例来解释这个式子,如下图所示。我们假设左下角的格子为最小值,那么有三种情况:
- 该值为0。则和前面组不成正方形,dp[i]=0+1=1。
- 该值为1。则其它值只能大于等于1,若都是等于1,说明周围三个小正方形没办法和其它正方形组成更大的正方形,所以只能它们4个组成。
- 该值为大于1的数,假设为2。则代表该蓝色格子与其左侧、左上侧、上侧组成了一个边长为2的正方形,由于黑色和绿色都大于2,所以黑色格子的左上角和上侧、绿色格子的上侧都不是0,于是就可以组成一个3*3的正方形,也即边长=2+1=3。其它大小以此类推。
上面的时间复杂度为O(mn),空间复杂度为O(mn)。接下来,我们可以对其进行优化。在上面的方法中,计算第i行的dp只用到了上一个元素和第i-1行,因此我们可以使用一维dp来满足要求。在扫描一行原始矩阵元素的时候,根据公式dp[j]=min(dp[j−1],dp[j],prev)来更新dp,其中prev是dp[j-1]。对于每一行,我们执行一遍过程,最后输出最大值即可。新的方法时间复杂度为O(mn),空间复杂度为O(n)。
代码实现
int min3(int a, int b, int c)
{
return (a < b ? (a < c ? a : c) : (b < c ? b : c));
}
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.empty())
return 0;
int rows = matrix.size();
int cols = matrix[0].size();
vector<int> dp(cols + 1, 0);
int maxr = 0, prev = 0;
for (int i = 1; i <= rows; i++)
{
for (int j = 1; j <= cols; j++)
{
int temp = dp[j];
if (matrix[i - 1][j - 1] == '1')
{
dp[j] = min3(dp[j - 1], prev, dp[j]) + 1;
maxr = max(maxr, dp[j]);
}
else
{
dp[j] = 0;
}
prev = temp;
}
}
return maxr * maxr;
}
复杂度分析
时间复杂度为O(mn),空间复杂度为O(n)。



文章评论