2019年牛客网校招全国同一模拟笔试（5月场）部分题目解析

一、选择题部分

1.有关多线程，多进程的描述错误的是

A.子进程获得父进程的数据空间，堆和栈的复制品
B.线程可以与同进程的其他线程共享数据，但是它拥有自己的栈空间且拥有独立的执行序列
C.线程执行开销小，但是不利于资源管理和保护
D.进程适合在SMP机器上进行，而线程则可以跨机器迁移

解析：

对于A选项来说，创建子进程的时候，子进程会复制父进程用户空间的所有数据，子进程会复制父进程内核空间PCB中绝大多数数据（少部分例如进程ID、父进程的ID等数据不会复制）。数据空间、堆、栈都是在用户空间，故A选项正确。

对于B、C选项，在学习的时候有这句话原话，直接记住就好，D选项其实也有原话，但是下面解释一下。

SMP（Symmetric Multi Processing）是对称多处理系统，这种系统最大的特点就是共享所有资源；与之相对的是MPP

SMP是Symmetric Multi Processing的简称，意为对称多处理系统，内有许多紧耦合多处理器，这种系统最大的特点就是共享所有资源。（Massively Parallel Processing），意为大规模并行处理系统，这样的系统是由许多松耦合处理单元组成的，这里指的是处理单元而不是处理器。每个单元内的CPU都有自己私有的资源，如总线、内存、硬盘灯。在每个单元内都有操作系统和管理数据库的实例副本。这种结构最大的特点在于不共享资源。

因而线程更适合在SMP机器上进行，而进程则可以跨机器迁移。

2.关于线程描述正确的是？

进程是具有一定独立功能的程序关于某个数据集合上的一次运行活动，进程是系统进行资源分配和调度的一个独立单位。

线程是进程的一个实体，是CPU调度和分派的基本单位，它是比进程更小的能独立运行的基本单位。线程自己基本上不拥有系统资源，只拥有一点在运行中必不可少的资源（如程序计数器,一组寄存器和栈），但是它可与同属一个进程的其他的线程共享进程所拥有的全部资源。

重点：计算机网络（OSI层次、TCP/IP、数据包、UDP、子网划分、HTTP、HTTPS、TCP套接字和UDP套接字等）、加密解密算法（RSA等）、操作系统（进程、线程、操作系统调度、多进程多线程操作等）。

编程题一：牛牛数星星

牛牛把星星图看成一个平面，左上角为原点（坐标(1,1)）。现在又n颗星星，他给每颗星星都标上坐标(xi,yi)，问m个问题，给你两个坐标(a1,b1)和(a2,b2)表示一个矩形的左上角和右下角。在这个矩形里面有多少个星星？（边界上的星星也算矩形内的）。

输入：

第一行输入n：星星数
接下来n行，每行两个值分别代表星星的坐标，(1<=xi,yi,<=1000)
然后输入m：表示m个问题
接下来m行，每行4个数字分别代表a1,b1,a2,b2。

输出：

输出m行分别代表m个问题的答案。

做题时的思路

做题的时候我思考的更多是如何直接去解决这个问题，并没有观察一些规律。我当时的想法很简单，就是在这个矩形里进行遍历。

我首先新建一个1001*1001的矩阵，然后第0行和第0列全部置零（我是考虑因为题目说从坐标（1,1）开始，为了转换麻烦所以把第0行第0列置空，从第1行第1列开始），然后把所有对应星星的坐标处的值全部置为1，这样没有星星的地方全部为0。

然后针对每个问题，设置一个temp=0，遍历两个坐标所围成的矩形，然后判断当前点是否为1，如果为1则++temp，最后得到的temp值就为所需要的答案。

这个方法时间复杂度为O(n^3)，在实际运行中，通过率80%，显然出现了超时问题。

思路优化版本

我上面这个版本其实非常糟糕，因为最多我们可能有10万颗星星，也就达标者最多10万次的查询，O(n^3)是非常可怕的。我们可以换一种思路。

如下图，是这个想法的一个总的示意图，右下角红色加粗黑框里面就是我们要求的矩形部分。

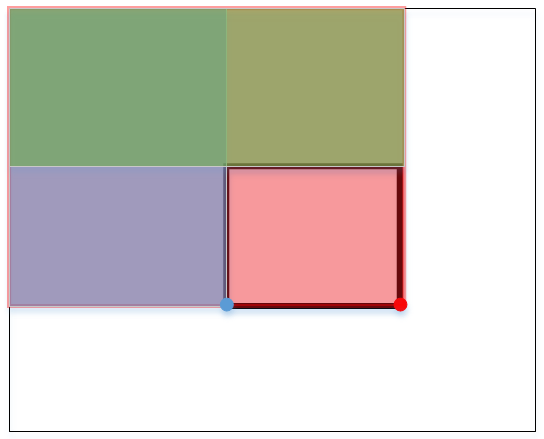
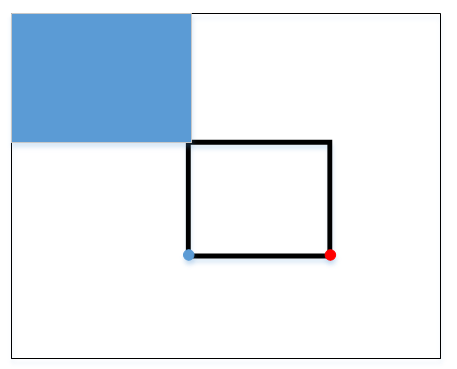
我们首先找这个点左上方有多少个星星，就是下图所示，至于我们为什么要求这部分面积，后面就知道了。

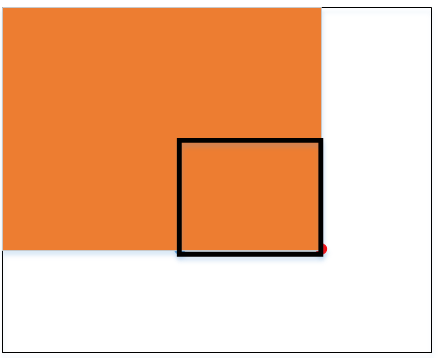
然后我们还可以求矩形右下角左上方里面的点，如下橘色部分所示

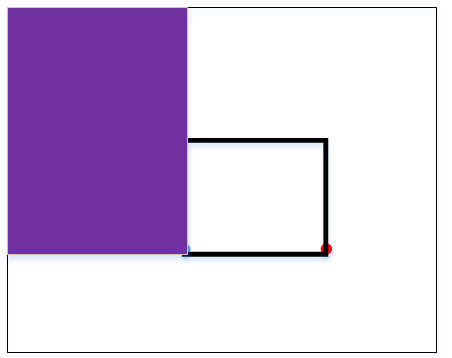
然后再求矩形左下角那个点的左上方的部分，如下图紫色所示。

再求矩形右上角左上方的部分，如下图绿色所示。

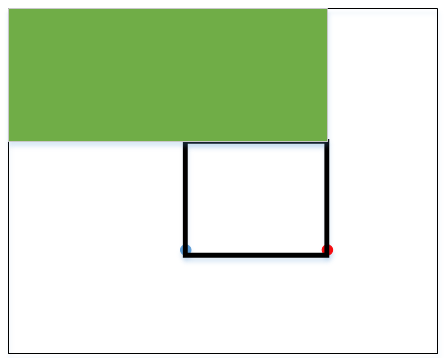
然后你就会发现下面两个点：

1. 上面求各个矩形里面的有多少个星星，实际上都是求某一点左上方一直到边界有多少颗星星，这说明它们可以用同样的递推公式来求解。
2. 我们所要求的的红色黑框部分的里面的星星=橘色框里面的星星-紫色框里面的星星-绿色框里面的星星+蓝色框里面的星星（因为紫色框和绿色框的重叠部分是蓝色框，所以蓝色框被多减了一次）。

那么实际上这样，我们只需要遍历一次1000*1000的地图就行了，每个查询可以O（1）来获取。实际复杂度降为了O(n^2)，大小还算可以接受。

代码实现（做题时的版本）

int main()
{
    long n,m;
    int x, y, a1, b1, a2, b2;
    cin >> n;
    vector<int>rows(1001, 0);
    vector<vector<int> > matrix(1001, rows);
    for (long i = 0; i < n; i++)
    {
        cin >> x >> y;
        matrix[x][y] = 1;
    }
    cin >> m;
    vector<int>result(m, 0);
    for (int i = 0; i < m; i++)
    {
        cin >> a1 >> b1 >> a2 >> b2;
        int temp=0;
        for (int j = a1; j <= a2; j++)
        {
            for (int k = b1; k <= b2; k++)
            {
                if (matrix[j][k] == 1)
                    ++temp;
            }
        }
        result[i] = temp;
    }
    //test
    for (int i = 0; i < m; i++)
    {
        cout << result[i] << endl;
    }
    //system("pause");
    return 0;
}

代码实现（优化版本）

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int maxx = 1005;
    int n, m;
    int x, y, a1, b1, a2, b2;
    vector<int>rows(maxx, 0);
    vector<vector<int> > matrix(maxx, rows);//标志该位置是否有星星，有为1，没有为0
    vector<vector<int> >num(maxx, rows);//点的坐标为num的x和y值，这一矩阵上的每一个点的值为左上方的星星点数
    cin >> n;
    //第一步：存入值
    for (int i = 0; i < n; i++)
    {
        cin >> x >> y;
        matrix[x][y] = 1;
    }
    //计算Num的值
    for (int i = 1; i < maxx; i++)
    {
        for (int j = 1; j < maxx; j++)
        {
            num[i][j] = num[i - 1][j] + num[i][j - 1] + matrix[i][j] - num[i - 1][j - 1];
        }
    }
    cin >> m;
    vector<int>result;
    //红色黑框部分的里面的星星=橘色框里面的星星-紫色框里面的星星-绿色框里面的星星+蓝色框里面的星星
    for (int i = 0; i < m; i++)
    {
        cin >> a1 >> b1 >> a2 >> b2;;
        int temp = num[a2][b2] - num[a1 - 1][b2] - num[a2][b1 - 1] + num[a1 - 1][b1 - 1];
        result.push_back(temp);
    }
    for (int i = 0; i < m; i++)
        cout << result[i] << endl;

    //system("pause");
    return 0;
}

编程题2：牛牛与世界杯门票

牛牛叫n个小伙伴去莫斯科看世界杯，门票有m种套票，每种套票x元，包含y张门票，当然也可以单独购买门票，此时门票k元。请选择花费最少的方案。

输入

第一行输入n(0<=n<=999),m(1<=m<=1000),k(1<=k<=100000)。
接下来m行，每行输入xi(1<=xi<=100000）和yi(2<=yi<=1000)表示套餐价格和门票数量。

输出

最少花费的价格。

做题思路

我的做题思路是：

第一步，设置一个存储所有可能取到的价格的vector，命名为price。
第二步，计算方案1：全部采用单买门票方式，价格push进入price。
第三步，计算所有方案的性价比（包括只买门票的方式），并将它们按照单价从小到大排列。
第四步，新建变量sum，表示每个方案的结果，新建变量i，表示第i个方案。然后使用for循环，从第1个方案开始（i=0），判断是否符合i<m+1且剩余人数大于当前方案人数，若符合则将sum=sum+plan.value，剩余人数people=people-plan.person。
第五步，判断剩余人数people是否等于0，若等于0，将sum数值push进入price，然后执行第六步；否则，分别计算再购买第i到第m-1（计数从0开始）个方案的价格，共m-i+1个数，push进入price，同时还有一种方案是使用单独买票来补充，push进入price。
第六步，寻找sum中的最小值，即为最小的花费。

可能会存在第三到第五步里面重复了方案1，但是因为只是寻找最小值，所以重复也没关系。
时间复杂度是O(nlogn)，虽然时间复杂度较低，但是空间复杂度较高。而且只通过了30%。

优化版做题思路

这个题可以看做是一种完全背包问题。人的个数相当于背包的容量，票的价格相当于价值，dp[i]表示买到i张票时的最小花费为dp[i]，最后dp[n]就是买n张票时候的最小花费（n是加上牛牛自己）。这是采用动态规划来解决这个问题。
动态规划就是两种情况，当我们第i个人的时候，我们可以有这样两种思路：

• 当前人数i小于该方案的人数y，那就判断当前方案的结果和只采用套餐的结果哪个更实惠。
• 如果当前人数i大于等于该方案的人数y，那么就判断当前方案的结果和i-y个人用原来的方案，后面y个人用当前套餐哪个更实惠。

所以就可以写出下面的代码。

代码实现（自己的思路）

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
struct pack {
    int sprice;
    int num;
    double price;
}p[1001];
bool cmp(pack a, pack b)
{
    return a.price < b.price;
}
//假设实际有h个人，套餐已经按照平均价格从低到高进行了排序。我们要从平均价格最低的开始买，
int main()
{
    int n, m,ans;
    vector<int> price;//设置一个存储所有可能取到的价格的vector，命名为price。
    int k;
    cin >> n >> m >> k;//输入n个人，m个方案，单买票价k元
    //每个方案的总价、数量和单价
    for (int i = 0; i < m; i++)
    {
        cin >> p[i].sprice >> p[i].num;
        p[i].price = (double)(p[i].sprice / p[i].num);
    }
    //第二步：计算方案1：全部采用单买门票的方式，价格push进入price。
    int alldan = k*(n + 1);
    price.push_back(alldan);
    //第三步：把他们按照单价从小到大排列
    sort(p, p + m, cmp);
    //第四步：新建变量sum，表示每个方案的结果，新建变量i，表示第i个方案。
    int sum = 0;
    int i=0;
    int people = n + 1;
    for (; (i < m) && (people >= p[i].num); i++)
    {
        sum+=p[i].sprice;
        people -= p[i].num;
    }
    //第五步：判断剩余人数people是否等于0，若等于0，将sum数值push进入price，然后执行第六步
    if (people <= 0)
    {
        ans = min(alldan, sum);
    }
    else
    {
        //否则，分别计算再购买第i到第m-1（计数从0开始）个方案的价格，共m-i+1个数，push进入price
        int sum1 = sum;
        for (; i < m; i++)
        {
            sum += p[i].sprice;
            price.push_back(sum);
        }
        //同时还有一种方案是使用单独买票来补充，push进入price
        sum1 += people*k;
        price.push_back(sum1);
    }
    sort(price.begin(), price.end());
    ans = price[0];
    cout << ans << endl;
    return 0;
}

优化版代码

#include <iostream>
#include <vector>
#include<algorithm>
using namespace std;

int main()
{
    int n, m, k, x, y;
    vector<int>dp(1005,0);
    cin >> n >> m >> k;
    ++n;
    for (int i = 1; i <= n; i++)
    {
        dp[i] = i*k;
    }
    while (m--)
    {
        cin >> x >> y;
        for (int i = 1; i <= n; i++)
        {
            if (i - y >= 0)
                dp[i] = min(dp[i], dp[i - y] + x);
            else

                dp[i] = min(dp[i], x);
        }
    }
    int result = dp[n];
    cout << result << endl;
    system("pause");
    return 0;

}

编程题3：牛牛游玩记

又是晴朗的一天，牛牛的小伙伴们都跑来找牛牛去公园玩。但是牛牛想呆在家里看E3展，不想出去逛公园，可是牛牛又不想鸽掉他的小伙伴们，于是找来了公园的地图，发现公园是由一个边长为n的正方形构成的，公园一共有m个入口，但出口只有一个。公园内有一些湖和建筑，牛牛和他的小伙伴们肯定不能从他们中间穿过，所以只能绕行。牛牛想知道他需要走的最短距离并输出这个最短距离。

输入

第一行输入一个数字n(1≤n≤1000)表示公园的边长
接下来会给你一个n*n的公园地图，其中 . 表示公园里的道路，@表示公园的入口，*表示公园的出口，#表示公园内的湖和建筑。牛牛和他的小伙伴们每次只能上下
左右移动一格位置。
输入保证公园入口个数m(1≤m≤10000)且所有的入口都能和出口相连。

输出：

牛牛行走的最短距离

代码思路

这个题虽然有很多个入口，1个出口，但是我们可以很容易想到加上一个源点，将所有的入口与源点相连接，这样就形成一个我们熟悉的图像了。我们只要把所有起点在一开始就放入到深度优先搜寻的队列中，后面按照普通的深度优先（BFS）写即可。

代码实现

#include<queue>
#include<iostream>

using namespace std;

const int maxn = 1e3 + 5;

const int dx[] = { 0, 1, 0, -1 };
const int dy[] = { -1, 0, 1, 0 };

struct node {
    int x, y;
};
int n, m;
int dis[maxn][maxn];
char mp[maxn][maxn];
node a, ed;
int main() {
    memset(mp, 0, sizeof(mp));
    memset(dis, -1, sizeof(dis));
    queue<node> q;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> mp[i];
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (mp[i][j] == '@') {
                a.x = i;
                a.y = j;
                q.push(a);
                dis[i][j] = 0;
            }
            if (mp[i][j] == '*') {
                ed.x = i;
                ed.y = j;
            }
        }
    }
    while (q.size()) {
        node p = q.front();
        q.pop();
        for (int i = 0; i < 4; i++) {
            int px = p.x + dx[i];
            int py = p.y + dy[i];
            if (dis[px] == -1 && px >= 0 && px < n && py >= 0 && py < n && mp[px] != '#') {
                node pp;
                pp.x = px;
                pp.y = py;
                q.push(pp);
                dis[px] = dis[p.x][p.y] + 1;
                if (px == ed.x && py == ed.y)
                    break;
            }
        }
        if (dis[ed.x][ed.y] != -1) break;
    }
    cout << dis[ed.x][ed.y]<<endl;
    return 0;
}