题目1:机器人的运动范围
题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
题目解析
这个题可以看做是广度搜索优先(BFS)的一个拓展或者说是改编。如果说没有“不能进入行坐标和列坐标的数位之和大于****k****的格子”这个条件,那么它就是一个纯粹的BFS问题,设置上这个,就基本上就相当于只是多了一个条件。所以我们需要做的就是以下几个工作:
1.设置标志位。bool flags=new bool[rowscols]。
2.将移动一步单独设置为一个子函数,在这个函数里面,原始的判断条件只是:
if(i>=0 && i< rows && j >=0 && j<cols && flags[i*cols+j]==false)
而现在则变成了:
if(i>=0 && i< rows && j >=0 && j<cols && (gssum(i) + gssum(j) <= threshold) && flags[i*cols+j]==false)
代码
int movingCount(int threshold, int rows, int cols)
{
bool *flags=new bool[rows*cols];//所有格子的标志位默认设置为false
for(int i=0;i<rows*cols;i++)
flags[i]=false;
int count = movingstep(threshold, rows, cols, 0, 0, flags);;//记录可访问格子数量
return count;
}
int movingstep(int threshold, int rows, int cols, int i, int j, bool *flags)
{
int count = 0;
if(i>=0 && i< rows && j >=0 && j<cols && (gssum(i) + gssum(j) <= threshold) && flags[i*cols+j]==false)
{
flags[i*cols+j]=true;
count = 1 + movingstep(threshold, rows, cols, i+1, j, flags)+movingstep(threshold, rows, cols, i-1, j, flags)+movingstep(threshold, rows, cols, i, j+1, flags)+movingstep(threshold, rows, cols, i, j-1, flags);
}
return count;
}
int gssum(int i)
{
int sum = 0;
while(i)
{
sum += i % 10;;
i /= 10;
}
return sum;
}
题目2:把字符串转换成整数
题目描述
将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能,但是string不符合数字要求时返回0),要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。
题目解析
本题目其实是一个很简单的题目,只需要很细心判断以下几处问题即可:
1.不考虑最前面的空格;
2.若除去空格后的第一位为“+”或“-”,则分别将标志位做不同的设置,若为数字,直接将标志位设置为同“+”,若为其它则直接返回0;
3.后续几位直接判断是否为0~9之间的数字,由于是字符串格式,所以为ascii码,这样,我们在转换成int格式的时候,直接用该字符减去’0’即可。
代码
int StrToInt(string str) {
int len=str.length();
if(len==0)
return 0;
int i = 0;
int res = 0;
int fla = 1;
//滤掉前面的空格
while(str[i]==' '){
i++;
}
//进行符号判断
if(str[i]=='+'){
i++;
}else if(str[i]=='-'){
i++;
fla=-1;
}
while(str[i]!='\0'){
//对字符进行是否为数字的判断
if(str[i]>='0'&&str[i]<='9'){
res=res*10+fla*(str[i]-'0');
i++;
}else{
res=0;
break;
}
}
return res;
}
题目3:表示数值的字符串
题目描述
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。 但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。
题目解析
表示数值的字符串遵循的规则;
1.在数值之前可能有一个“+”或“-”,接下来是0到9的数位表示数值的整数部分,如果数值是一个小数,那么小数点后面可能会有若干个0到9的数字。
2表示数值的小数部分,如果用科学计数法表示,接下来是一个‘e’或者‘E’,以及紧跟着一个整数(可以有正负号)表示指数。
代码
bool isNumeric(char* string)
{
if(string == NULL)
return false;
if(*string == '+' || *string =='-')
string++;
if(*string =='\0')
return false;
int dot = 0;//小数点的个数
int num = 0;//数字的个数
int ex = 0;//e指数的个数
while(*string !='\0')
{
if((*string >= '0') && (*string <='9'))
{
num++;
string++;
}
//小数点开始
else if(*string =='.')
{
if(dot> 0 || ex > 0)
return false;
dot++;
string++;
}
//指数e
else if((*string =='e') ||(*string == 'E'))
{
if(num ==0 || ex > 0)
return false;
string++;
ex++;
if(*string == '+' || *string =='-')
string ++;
if(*string=='\0')
return false;
}
else
return false;
}
return true;
}
题目4:链表中环的入口节点
题目描述
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
题目解析
其实我的思路是把每个访问过的结点做标记,然后不断往下走后,遇到的第一个标记过的点,就是还的入口结点,如果没有遇到,则就不存在环,返回null。但是这种方法比较复杂,而且很难找到标志每个结点的特点在哪里。
所以可以这样考虑。如图4.1所示。
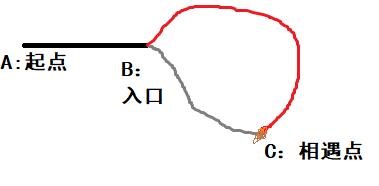
图4.1 示意图
我们假设x为AB之间的距离,a为从b到c的距离(顺时针移动),c为环的长度。我们可以设置两个指针,一个快一个慢,然后快的是慢的速度的两倍。设快指针为f,慢指针为s,则当快指针和慢指针相遇的时候,s=x+mc+a,f=x+nc+a,m和n为某不同的常数,s=f。所以x=(n-2m)c-a=(n-2m-1)c+c-a。n-2m-1可为0。这里为了处理方便,省略前面这个类似于周期的东西,只留下c-a。c-a是什么?c-a就是图4.1中灰色的这条线。也就是说,AB之间的距离=灰色的线。这样,我们可以再重新将f这个指针(也可以是s)指向A,那么当f和s相遇的时候,所在的结点就是入口结点。
代码
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
if((pHead==NULL)||(pHead->next==NULL)||(pHead->next->next==NULL))
return NULL;
ListNode* fast = pHead->next->next;
ListNode* slow = pHead->next;
//先判断有没有环
while(fast!=slow)
{
if((fast->next !=NULL) &&(fast->next->next!=NULL)){
fast=fast->next->next;
slow=slow->next;
}
else{
return NULL;
}
}
//如果能执行到这一步,说明有环,且此时fast==slow。
//然后把fast调整到头部,此时fast和slow第一次相遇的位置就是入口地址
fast=pHead;
while(fast!=slow)
{
fast=fast->next;
slow=slow->next;
}
return slow;
}
题目5:把二叉树打印成多行
题目描述
从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
题目解析
如果不加上“打印成多行”,那么这就是一个层序遍历,利用队列实现即可。而加上这个要求之后,只需要增加两个参数设置,当参数达到阈值后,输出第一行。
代码
vector<vector<int> > Print(TreeNode* pRoot) {
vector<vector<int> > vect;//最后输出的结果
if(pRoot==NULL)
return vect;//若pRoot为空,直接返回空
//接下来总体上就是一个层序遍历的变体,所以可以使用层序遍历进行修改完成此题目
//层序遍历可以利用队列来实现。
//首先新建一个队列,然后将链表的头push进去,然后弹出,获得头的值,然后再分别push进去其左右两个结点。然后弹出头上的
//然后判断其左右结点是否有,有就push进去。这样层序遍历其实就是用队列来输入输出。
queue<TreeNode*> tmp;
tmp.push(pRoot);
while(!tmp.empty())
{
int l=0;
int h=tmp.size();
vector<int> t;
while(l++<h)//按行输出
{
TreeNode* k = tmp.front();
tmp.pop();
t.push_back(k->val);
if(k->left)
tmp.push(k->left);
if(k->right)
tmp.push(k->right);
}
vect.push_back(t);
}
return vect;
}
题目6:按之字形顺序打印二叉树
题目描述
请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
题目解析
这个题目是对于题目5的拓展,我们依旧可以借鉴层序遍历,但是这里我们要使用的是两个堆栈。总体上是一样的。
假设我们输出第一行,那么按照顺序输出以后,push进堆栈的顺序要和之前的相反,这样push进入第二个堆栈。当用第二个堆栈输出的时候,就要先左后右push进入第一个堆栈。
代码
vector<vector<int> > Print(TreeNode* pRoot) {
vector<vector<int> > res;//结果存放
stack<TreeNode*> stackl,stackr;//从右往左和从左往右输出结果的堆栈
if(pRoot!=NULL)
{
stackl.push(pRoot);//跟层序遍历类似,先把根节点push进去
}
struct TreeNode* node;//中介的结点,类似于层序遍历
while(!stackl.empty() || !stackr.empty())
{
vector<int> tmp;
if(!stackl.empty()){
while(!stackl.empty())
{
node=stackl.top();
stackl.pop();
tmp.push_back(node->val);
if(node->left!=NULL)
stackr.push(node->left);
if(node->right!=NULL)
stackr.push(node->right);
}
res.push_back(tmp);
}
else if(!stackr.empty()){
while(!stackr.empty()){
node=stackr.top();
stackr.pop();
tmp.push_back(node->val);
if(node->right!=NULL)
stackl.push(node->right);
if(node->left!=NULL)
stackl.push(node->left);
}
res.push_back(tmp);
}
}
return res;
}
题目7:二叉搜索树的第k个节点
题目描述
给定一棵二叉搜索树,请找出其中的第k小的结点。例如, (5,3,7,2,4,6,8) 中,按结点数值大小顺序第三小结点的值为4。
题目解析
这个题看着挺唬人,实际非常简单。由于二叉搜索树本身就是具有顺序特点的二叉树,因此这个题实际上是中序遍历二叉搜索树,然后输出中序遍历的第k个值。
代码
class Solution {
private:
int count;
public:
void inorder(TreeNode* root, TreeNode* &ans)
{
if(root)
{
inorder(root->left,ans);
count--;//记录是第几个值
if(!count)
ans=root;
inorder(root->right,ans);
}
}
TreeNode* KthNode(TreeNode* pRoot, int k)
{
if(pRoot==NULL || k<1)
return NULL;
TreeNode* ans = NULL;
count = k;
inorder(pRoot, ans);
return ans;
}
};
题目8:翻转单词顺序
题目描述
牛客最近来了一个新员工Fish,每天早晨总是会拿着一本英文杂志,写些句子在本子上。同事Cat对Fish写的内容颇感兴趣,有一天他向Fish借来翻看,但却读不懂它的意思。例如,“student. a am I”。后来才意识到,这家伙原来把句子单词的顺序翻转了,正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行,你能帮助他么?
题目解析
这个题目其实最容易想到的就是,我们可以整个句子翻转过来,这样做的结果是,每个单词正好也都是反序的,我们只需要再调用一次翻转,将单词翻转就变成了正序。
代码
void ReversedWord(string &str, int st, int en)
{
while(st < en)
{
swap(str[st++],str[en--]);
}
}
string ReverseSentence(string str) {
int len = str.size();
int st = 0;
int en = 0;
ReversedWord(str,0,len-1);//先整体翻转
int i=0;
while(i < len)
{
while(i < len && str[i] == ' ') //空格跳过
i++;
en = st = i; //记录单词的第一个字符的位置
while(i < len && str[i] != ' ') //不是空格 找单词最后一个字符的位置
{
i++;
en++;
}
ReversedWord(str, st, en - 1); //局部翻转
}
return str;
}
题目9:扑克牌顺子
题目描述
LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张^_^)...他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿!!“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子.....LL不高兴了,他想了想,决定大\小 王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。 现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何, 如果牌能组成顺子就输出true,否则就输出false。为了方便起见,你可以认为大小王是0。
题目解析
顺子要求:
1.牌面不重复;
2.牌面是连续的。
为了满足以上条件,所以做了以下两个步骤:
1.设置flag。只要不重复,很多都会用到flag,由于扑克牌里面有14种牌,所以flag数组长度为14,默认为0,有重复就加1。
2.寻找最大最小值,计算它们的差值,判断结果。由于牌面不重复,又由于只有五张,所以max-min<5的时候(其实就是为4的时候),肯定是连续的,若大了,肯定不连续。
代码
bool IsContinuous( vector<int> numbers ) {
if(numbers.empty())
return false;
int count[14]={0};
int max = -1;
int min = 14;
for(int i=0;i<numbers.size();i++)
{
count[numbers[i]]++;
if(numbers[i]==0)
continue;
if(count[numbers[i]]>1)
return false;
if(numbers[i] > max)
max = numbers[i];
if(numbers[i] < min)
min = numbers[i];
}
if(max - min <5)
return true;
return false;
}
题目10:矩阵中的路径
题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
题目解析
类似于题目3,在此就不具体说了。
代码
private:
bool isPath(char *matrix, vector<char> flags, char* str, int i, int j, int rows, int cols)
{
if(i<0|| i>=rows || j<0 || j>=cols)
return false;
if(matrix[i*cols+j] == *str && flags[i*cols+j]==0)
{
flags[i*cols+j]=1;
if(*(str+1)==0)
return true;
bool cond = isPath(matrix,flags,(str+1),i,j-1,rows,cols) ||
isPath(matrix,flags,(str+1),i-1,j,rows,cols)||
isPath(matrix,flags,(str+1),i,j+1,rows,cols)||
isPath(matrix,flags,(str+1),i+1,j,rows,cols);
if(cond==false)
flags[i*cols+j]=0;
return cond;
}
else
return false;
}
public:
bool hasPath(char* matrix, int rows, int cols, char* str)
{
vector<char> flags(rows*cols,0);
bool con = false;
for(int i=0;i<rows;i++)
for(int j =0;j<cols;j++)
{
con = (con|| isPath(matrix,flags,str,i,j,rows,cols) );
}
return con;
}


文章评论