Leetcode 309:最佳买卖股票时机含冷冻期
题目描述
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
解题思路
这又是一个动态规划问题,我们思考该题的状态图。一共可能有三个状态:
- Hold:购入股票;
- Sold:卖出股票;
- Rest:持有股票什么都不做。
那么如何能得到这三个状态呢?
对于Hold来说:
- 前一天持有,当日Rest;
- 前一天Rest,当日买入股票。
对于Sold来说:
- 前一日Hold股票,当日卖出。
对于Rest来说:
- 前一日Sold了,当日必须Rest;
- 也可以前一天Rest,当日继续Rest。
所以说状态转换图如下:
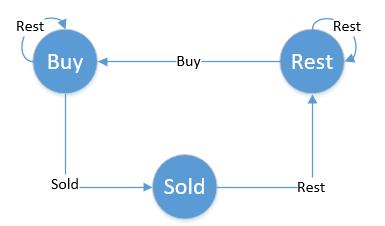
由上面的状态转换图我们可以得到:
(以下i表示第i天,i-1代表前一天)
sold[i]=hold[i-1]+price[i];
hold[i]=max(hold[i-1],rest[i-1]-price[i]);
rest[i]=max(rest[i-1],sold[i-1]);
那么对于最后一天来说,最大值存在两种情况:什么都不做;卖出股票。所以为max(sold,rest)。
代码实现
int maxProfit(vector<int>& prices) {
int sold=0,hold=INT_MIN,rest=0;
for(int price:prices){
int pre_sold=sold;
sold=hold+price;
hold=max(hold,rest-price);
rest=max(rest,pre_sold);
}
return max(sold,rest);
}
复杂度分析
时间复杂度:O(n)
LeetCode 312:戳气球
题目描述
n 个气球,编号为0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。每当你戳破一个气球 i 时,你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
你可以假设 nums[-1] = nums[n] = 1,但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例
输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 315 + 358 + 138 + 181 = 167
解题思路
这个题类似于游艇租赁问题,游艇租赁问题就是找分隔点,而本题也是类似的。这种动态规划问题和我们前面遇到的是不太一样的。
动态规划问题就是将一个大问题分隔成多个独立的小问题。在这个问题上,就是我们可以将大的区间分隔为独立的小区间,然后先戳爆小区间,也就是先算小区间,再组合出大区间。
对于本题的示例[3,1,5,8]来说,步骤如下:
第一步:计算长度为1的区间,分别戳3,1,5,8。
第二步:计算长度为2的区间,分别算[3,1],[1,5],[5,8]:
对于3,1:3最后戳,1已经算出;同样1最后戳,3也算出;
对于1,5:1最后戳,5已经算出;同样5最后戳,1也算出;
对于5,8:5最后戳,8已经算出;同样8最后戳,5也算出。
第三步,计算长度为3的区间,分别计算[3,1,5]和[1,5,8]:
对于3,1,5来说,3最后戳,1/5已经计算出来;1最后戳,3/5已经计算出来;5最后戳,3,1已经计算出来;
对于1,5,8来说,1最后戳,5/8已经计算出来;5最后戳,1/8已经计算出来;8最后戳,1,5已经计算出来。
第四步,计算长度为4的区间,即[3,1,5,8]:3最后戳,1,5,8已经算出。1最后戳3和5,8已经算出。5最后戳,3,1和8已经算出。8最后戳,3,1,5已经算出。
简单来说,写一个伪代码:
序列为num,[i,j]为区间,dp[i][j]为dp数组;c为区间长度,则
for(c in [1,N]){
for(i in [1,N-c+1])//区间起始点在[1,N-c+1]这个区间里面
{
j=i+c-1;//区间长度为c-1,即代表分别计算1,2,...,N的长度区间
for(k in [i,j]){
dp[i][j]=max(num[i-1]*num[k]*num[j+1])+dp[i][k-1]+dp[k+1][j]);
//当前戳中的值+其左侧戳中的值+其右侧戳中的值
}
}
}
解析参考自:
https://leetcode-cn.com/problems/burst-balloons/solution/san-chong-jie-fa-by-jason-2-6/
代码实现
int maxCoins(vector<int>& nums) {
int N;
N = nums.size();
nums.insert(nums.begin(), 1);
nums.push_back(1);//在开头和结尾插入1,因为题目说-1和最后一个位置当做1
const int len = nums.size();
vector<vector<int>> dp(len, vector<int>(len, 0));
for (int i = 1; i <= N; ++i) {
for (int j = 1; j + i - 1 <= N; ++j) {
const int k = j + i - 1;
int& ans = dp[j][k];
for (int m = j; m <= k; ++m) {
ans = max(ans, nums[j - 1] * nums[m] * nums[k + 1] + dp[j][m - 1] + dp[m + 1][k]);
}
}
}
return dp[1][N];
}
复杂度分析


文章评论