leetcode9: Palindrome(回文数)
题目描述
判断一个整数是否是回文数。
题目解析
我们通过观察可以看出,回文数有以下两种类型:ABA和ABBA。所以本质上它们都还是镜像对称的,所以可以想到一个结构,就是队列。我们可以把数字以中间位为对称轴拆成两部分,然后做下面这几步:
- 按顺序将对称轴右侧的几位push到一个queue里面(比如上面中的A/BA,剩下的就是AB/AB)。
- 然后判断这个数字的长度是奇数还是偶数,若是偶数,直接到下一步,若是奇数,操作
x /=10,也就是把对称轴删掉(这样X剩下的就是A/AB了)。 - 然后将queue里面的数字按pop的顺序连起来,判断与原来那个数字剩下的几位是否相等,若相等就是回文数。
代码实现
bool isPalindrome(int x) {
if (x < 0)
return false;
queue<int> tmp;
int len = 0;
int copy = 0;
//1.计算数字的长度
for (int i = x; i; i /= 10)
++len;
//2.按顺序将对称轴右侧的push到queue中。
for (int j = len / 2; j > 0; --j)
{
tmp.push(x % 10);
x /= 10;
}
//3.若是奇数,则提取出来对称轴前面的数字
if (len % 2 == 1)
x /= 10;
//4.把pop出来的数字连起来
for (int j = len / 2; j > 0; j--)
{
copy = copy * 10 + tmp.front();
tmp.pop();
}
//5.与x剩下的部分对比
if (copy == x)
return true;
else
return false;
}
Leetcode 1:Two sum
题目描述
Given an array of integers, find two numbers such that they add up to a specific target number.
The function twoSum should return indices of the two numbers such that they add up to the target, where index1 must be less than index2. Please note that your returned answers (both index1 and index2) are not zero-based.
You may assume that each input would have exactly one solution.
Input: numbers={2, 7, 11, 15}, target=9
Output: index1=1, index2=2
代码解析
代码实现
vector<int> twoSum(vector<int> &numbers, int target) {
vector<int>result;
int nlen = numbers.size();
if (nlen < 2)
return result;
vector<int>num;
for (int i = 0; i < nlen; i++)
{
num.push_back(numbers[i]);
}
sort(numbers.begin(), numbers.end());
int i = 0, j = nlen - 1,tmp1=INT_MIN,tmp2=INT_MIN;
while (i < j)
{
if (numbers[i] + numbers[j] == target)
{
tmp1 = numbers[i];
tmp2 = numbers[j];
break;
}
else if (numbers[i] + numbers[j] < target)
++i;
else if (numbers[i] + numbers[j] > target)
--j;
}
for (int k = 0; k < nlen; k++)
{
if (num[k] == tmp1)
{
result.push_back(k + 1);
continue;
}
if (num[k] == tmp2)
result.push_back(k+1);
}
sort(result.begin(), result.end());
return result;
}
代码2:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int>res(2,-1);
map<int,int> tmp;
for(int i=0;i<nums.size();i++)
{
if(tmp.count(target-nums[i]))
{
res[0]=tmp[target - nums[i]];
res[1]=i;
break;
}
tmp[nums[i]]=i;
}
return res;
}
Leetcode 50:计算x的n次幂
题目描述
实现pow(x,n),即计算x的n次幂函数。
题目解析
在剑指offer之中,我们可以使用二进制移位来实现相应的功能,但实际上,当数字过大的时候,这个方法已经不能使用了。这个时候我们可以用二分法。步骤如下:
- 依旧是先判断n是不是小于零,若是,令x等于原来的倒数,n变为原来的绝对值;否则不变,然后进入第2步。
- 执行一个fastPow()函数,这个函数是递归调用执行。首先如果此时n=0了,那么自然结果就是1.0;然后递归调用
half=fastPow(x,n/2),这实际上就是计算x的n/2次方的结果,然后这个时候判断n是奇数还是偶数,如果是偶数,那自然x的n次方就等于x的n/2次方乘x的n/2次方;如果是奇数,则结果就等于x的n次方就等于x的n/2次方乘x的n/2次方再乘x。
代码实现
double fastPow(double x, long long n)
{
if (n == 0)
return 1.0;
double half = fastPow(x, n / 2);
if (n % 2 == 0)
return half*half;
else
return half*half*x;
}
double myPow(double x, int n) {
if (x == 1.0)
return x;
if (n == 0)
return 1.0;
long long N = n;
if (N < 0)
{
x = 1 / x;
N = -N;
}
return fastPow(x, N);
}
leetcode 69:x的平方根(sqrt of x)
题目描述
实现int sqrt(int x)函数,计算并返回x的平方根,其中x是非负整数。由于返回类型是整数,所以结果只保留整数部分,将小数部分舍去。
题目解析
所以我们要做的事情就是让这个x(n+1)不断逼近x。由于只要求保留到整数,所以误差可以选择大一点,比如误差到0.5就可以结束逼近了。所以代码实现如下。
代码实现
int mySqrt(int x) {
if(x<0)
return -1;
double res=1.0;
if(x==0||x==1)
return x;
while(fabs(res*res-x)>0.5)
{
res=(res+x/res)/2;
}
return int(res);
}
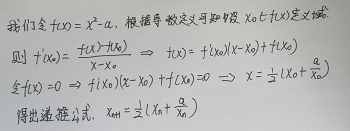


文章评论