汉诺塔问题

有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆环，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：
每次只能移动一个圆盘；大盘不能叠在小盘上面。

提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。

问：如何移？最少要移动多少次？

为了解决这个问题，不妨假设已经知道怎样移动N-1个圆环了。现在，为了把起点盘上的圆环移动到目标盘，需要做如下操作：

1、把N-1个圆环从起点盘移动到（当前）没有任何圆环的过度盘；
2、把最后一个圆环从起点盘移动到目标盘；
3、把N-1个圆环从国度盘移动到目标盘（模仿1和2的操作方法来实现）。

可以借助网友的图示，如果三个圆盘的话：

如果四个圆盘的话：

代码实现如下：

void hannoi(int n, char A, char B, char C)
{
    if (n == 1)
    {
        //把最后一个圆环从起点盘移动到目标盘
        cout << "移动圆盘" << n << "从盘" << A << "盘" << C << endl;
    }
    else
    {
        hannoi(n - 1, A, C, B);
        //把N-1个圆环从起点盘移动到（当前）没有任何圆环的过度盘；通过B、C盘在此函数调用中调用位置的互换，来实现把N-1个圆环从A盘到B盘的转移【A--B】。
        cout << "移动圆圈" << n << "从盘" << A << "盘" << C << endl;
        hannoi(n - 1, B, A, C);
        // 把N-1个圆环从过渡盘移动到目标盘（模仿1和2的操作方法来实现）；通过A、B盘在此函数调用中位置的互换，来实现N-1个圆环从B盘到C盘的转移【B--C】。
    }
}

若输入n=3，则结果如下：

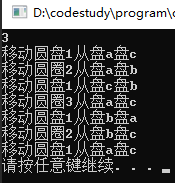
记不住想下面的口诀：递归-句子-递归。
两个盘子：先把小的由A移到B（ACB递归），然后把大的由A移到C（AC句子），然后把小的由B移到C（BAC递归）。