题目6 第一次只出现一次的字符
题目描述
在一个字符串(0<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1(需要区分大小写)。
题目解析
只要这种问题,就可以想到HashTable,但是由于这个问题很简单,而且字符串全部由字母组成,那么每个字母的ASCII码肯定不一样,我们就可以用一个长度为52的数组来记录他们出现的次数,对于字母每出现一次,就对它加1。
当然我们这里为了通用性,可以使用对任意字符进行判断,那么我们就可以考虑实现一个简单的哈希表。字符是一个长度为8的数据类型,所以有256种可能,于是可以创建一个长度为256的数组,每个字符根据其ASCII码值作为数组的下表对应数组的一个数字,而数组中存储的是每个字符出现的次数。
第一次扫描时,在河西表中更新一个字符出现的次数的时间是O(1)。如果字符串长度为n,那么第一次扫描的时间复杂度是O(n)。第二次扫描时,同样在O(1)时间内能独处一个字符出现的次数,所以时间复杂度仍然是O(n)。这样算起来,总的时间复杂度是O(n)。同时,我们需要一个包含256个字符的辅助数组,它的代销为1kb。由于这个数组的大小是一个常数,因此可以认为空间复杂度为O(1)。
代码
int FirstNotRepeatingChar(string str) {
int asc[256]={0};
int len=str.size();
if(len==0)
return -1;
for(int i=0;i<len;i++)
asc[str[i]]++;
for(int i=0;i<len;i++)
{
if(asc[str[i]]==1)
return i;
}
return -1;
}
题目7 丑数
题目描述
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
题目解析
代码1中所述是最简单的判断方法,很直观,但是效率不够高。
代码1
bool isUgly(int number)
{
while(number%2==0)
number/=2;
while(number%3==0)
number/=3;
while(number%/5==0)
number/=5;
return (number==1)?true:false;
}
int GetUglyNumber(int index)
{
if(index<=0)
return 0;
int number=0;
int uglyFound=0;
while(uglyFound<index)
{
++number;
if(isUgly(number))
{
uglyFound++;
}
}
return number;
}
题目8 数字在排序数组中出现的次数
题目描述
统计一个数字在排序数组中出现的次数。
题目解析
最简单的方法就是直接for循环,这个复杂度是O(n)。
代码
int GetNumberOfK(vector<int> data ,int k) {
int len = data.size();
int count=0;
for(int i=0;i<len;i++)
{
if(data[i]==k)
++count;
}
return count;
}
题目9 两个链表的第一个公共节点
题目描述
输入两个链表,找出它们的第一个公共结点。
代码
ListNode* FindFirstCommonNode( ListNode *pHead1, ListNode *pHead2) {
int len1 = findListLenth(pHead1);
int len2 = findListLenth(pHead2);
//如果两个长度不相等,就把长的那个链表上的指针从开头往后移动|len1-len2|个位置,这样就相当于两个链表同一起跑线开始。
if(len1 > len2){
pHead1 = walkStep(pHead1,len1 - len2);
}else{
pHead2 = walkStep(pHead2,len2 - len1);
}
//由于这个时候两个链表从指针所在位置往后长度肯定一致,所以这里指定pHead1和pHead2判断是否到尾部都可以
while(pHead1 != NULL){
//如果两个结点相等,自然就是第一个公共节点了,否则往后继续找
if(pHead1 == pHead2) return pHead1;
pHead1 = pHead1->next;
pHead2 = pHead2->next;
}
return NULL;
}
int findListLenth(ListNode *pHead1){
if(pHead1 == NULL) return 0;
int sum = 1;
while(pHead1 = pHead1->next) sum++;
return sum;
}
ListNode* walkStep(ListNode *pHead1, int step){
while(step--){
pHead1 = pHead1->next;
}
return pHead1;
}
题目10 数组中的逆序对
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
题目解析
我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候,我们不拿ta和后面的每一个数字作比较,否则时间复杂度就是O(n^2),因此我们可以考虑先比较两个相邻的数字。
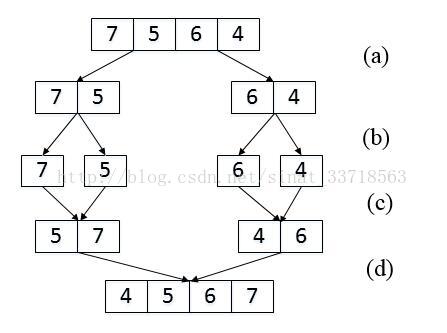
(a) 把长度为4的数组分解成两个长度为2的子数组;
(b) 把长度为2的数组分解成两个成都为1的子数组;
(c) 把长度为1的子数组 合并、排序并统计逆序对 ;
(d) 把长度为2的子数组合并、排序,并统计逆序对;
在上图(a)和(b)中,我们先把数组分解成两个长度为2的子数组,再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组,一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5,因此(7,5)组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对(6,4)。由于我们已经统计了这两对子数组内部的逆序对,因此需要把这两对子数组 排序 如上图(c)所示, 以免在以后的统计过程中再重复统计。
接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。
我们先用两个指针分别指向两个子数组的末尾,并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字,则构成逆序对,并且逆序对的数目等于第二个子数组中剩余数字的个数,如下图(a)和(c)所示。如果第一个数组的数字小于或等于第二个数组中的数字,则不构成逆序对,如图b所示。每一次比较的时候,我们都把较大的数字从后面往前复制到一个辅助数组中,确保 辅助数组(记为copy) 中的数字是递增排序的。在把较大的数字复制到辅助数组之后,把对应的指针向前移动一位,接下来进行下一轮比较。
过程:先把数组分割成子数组,先统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序。如果对排序算法很熟悉,我们不难发现这个过程实际上就是归并排序。
代码
int InversePairs(int* data, int length)
{
if(data==nullptr||length<0)
return 0;
int* copy=new int[length];
for(int i=0;i<length;++i)
copy[i]=data[i];
int count=InversePairsCore(data,copy,0,length-1);
delete[] copy;
return count;
}
int InversePairsCore(int*data,int*copy,int start,int end)
{
if(start==end)
{
copy[start]=data[start];
return 0;
}
int length=(end-start)/2;
int left=InversePairsCore(copy,data,start,start+length);
int right=InversePairsCore(copy,data,start+length+1,end);
//i初始化为前半段最后一个数字的下标
int i=start+length;
//j初始化为后半段最后一个数字的下标
int j=end;
int indexCopy=end;
int count=0;
while(i>=start&&j>=start+length+1)
{
if(data[i]>data[j])
{
copy[indexCopy--]=data[i--];
count+=j-start-length;
}
else
{
copy[indexCopy--]=data[j--];
}
}
for(;i>=start;--i)
copy[indexCopy--]=data[i];
for(;j>=start+length+1;--j)
copy[indexCopy--]=data[j];
return left+right+count;
}


文章评论